本文针对传统 PnP 方法与深度学习的结合做了一些工作，整体思路比较简单，主要就是怎么把传统方法 PnP 的残差反向传播给神经网路，从而能够实现 End2End 的训练，以及无需给定数据关联下的计算（Blind PnP）。

1 Backpropagating a PnP solver (BPnP)

首先用数学语言描述 PnP 问题。

定义 g 是一个 PnP solver，其输出 y 是求解的 6DoF 姿态：

\(\boldsymbol{y}=g(\boldsymbol{x}, \boldsymbol{z}, \mathbf{K})\tag{1}\)

其中 x 代表特征点在图像上的 2D 坐标观测，z 代表空间中的 3D 点坐标， 代表一一对应的一对映射，K是相机内参：

\(\begin{array}{l}
\boldsymbol{x}=\left[\begin{array}{llll}
\boldsymbol{x}_{1}^{T} & \boldsymbol{x}_{2}^{T} & \ldots & \boldsymbol{x}_{n}^{T}
\end{array}\right]^{T} \in \mathbb{R}^{2 n \times 1} \\
\boldsymbol{z}=\left[\begin{array}{llll}
\boldsymbol{z}_{1}^{T} & \boldsymbol{z}_{2}^{T} & \ldots & \boldsymbol{z}_{n}^{T}
\end{array}\right]^{T} \in \mathbb{R}^{3 n \times 1}
\end{array}\tag{2}\)
其实求解 PnP 就是这样一个最优化问题：

\(\boldsymbol{y}=\underset{\boldsymbol{y} \in S E(3)}{\arg \min } \sum_{i=1}^{n}\left\|\boldsymbol{r}_{i}\right\|_{2}^{2}\tag{3}\)
其中 \(\boldsymbol{\pi}_{i}=\pi\left(\boldsymbol{z}_{i} \mid \boldsymbol{y}, \mathbf{K}\right)\) 是投影函数，\(\boldsymbol{r}_{i}=\boldsymbol{x}_{i}-\boldsymbol{\pi}_{i}\) 是重投影误差。

则通过如下简写：

\(\boldsymbol{y}=\underset{\boldsymbol{y} \in S E(3)}{\arg \min } \quad\|\boldsymbol{x}-\boldsymbol{\pi}\|_{2}^{2}\tag{4}\)
其中：

\(\boldsymbol{\pi}:=\left[\boldsymbol{\pi}_{1}^{T}, \ldots, \boldsymbol{\pi}_{n}^{T}\right]^{T}\tag{5}\)

1.1 隐函数求导

1.2 Constructing the constraint function f

定义 PnP 的目标函数为：

\(o(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}, \mathbf{K})=\sum_{i=1}^{n}\left\|\boldsymbol{r}_{i}\right\|_{2}^{2}\tag{6}\)
目标函数取极小值，则有：

\(\left.\frac{\partial o(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}, \mathbf{K})}{\partial \boldsymbol{y}}\right|_{\boldsymbol{y}=g(\boldsymbol{x}, \boldsymbol{z}, \mathbf{K})}=\mathbf{0}\tag{7}\)
我们这样定义：

\(f(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}, \mathbf{K})=\left[f_{1}, \ldots, f_{m}\right]^{T}\tag{8}\)
其中：

\(\begin{aligned}
f_{j} &=\frac{\partial o(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z}, \mathbf{K})}{\partial y_{j}} \\
&=2 \sum_{i=1}^{n}\left\langle\boldsymbol{r}_{i}, \frac{\partial \boldsymbol{r}_{i}}{\partial y_{j}}\right\rangle \\
&=\sum_{i=1}^{n}\left\langle\boldsymbol{r}_{i}, \boldsymbol{c}_{i j}\right\rangle \\
\boldsymbol{c}_{i j} &=-2 \frac{\partial \boldsymbol{\pi}_{i}}{\partial y_{j}}
\end{aligned}\tag{9}\)

1.3 Forward and backward pass

我们首先重写 PnP 的函数，引入初始姿态 \(y^{(0)} \)：

\(\boldsymbol{y}=g\left(\boldsymbol{x}, \boldsymbol{z}, \mathbf{K}, \boldsymbol{y}^{(0)}\right)\tag{10}\)
根据隐函数求导法则有：

\(\begin{aligned}
\frac{\partial g}{\partial \boldsymbol{x}} &=-\left[\frac{\partial f}{\partial \boldsymbol{y}}\right]^{-1}\left[\frac{\partial f}{\partial \boldsymbol{x}}\right] \\
\frac{\partial g}{\partial \boldsymbol{z}} &=-\left[\frac{\partial f}{\partial \boldsymbol{y}}\right]^{-1}\left[\frac{\partial f}{\partial \boldsymbol{z}}\right] \\
\frac{\partial g}{\partial \mathbf{K}} &=-\left[\frac{\partial f}{\partial \boldsymbol{y}}\right]^{-1}\left[\frac{\partial f}{\partial \mathbf{K}}\right]
\end{aligned}\tag{11}\)
对于神经网络我们可以获得输出的梯度 \(\nabla \boldsymbol{y}\)，则各个输入梯度为：

\(\begin{aligned}
\nabla \boldsymbol{x} &=\left[\frac{\partial g}{\partial \boldsymbol{x}}\right]^{T} \nabla \boldsymbol{y} \\
\nabla \boldsymbol{z} &=\left[\frac{\partial g}{\partial \boldsymbol{z}}\right]^{T} \nabla \boldsymbol{y} \\
\nabla \mathbf{K} & =\left[\frac{\partial g}{\partial \mathbf{K}}\right]^{T} \nabla \boldsymbol{y}
\end{aligned}\tag{12}\)

1.4 Implementation notes

2 End-to-end learning with BPnP

2.1 Pose estimation

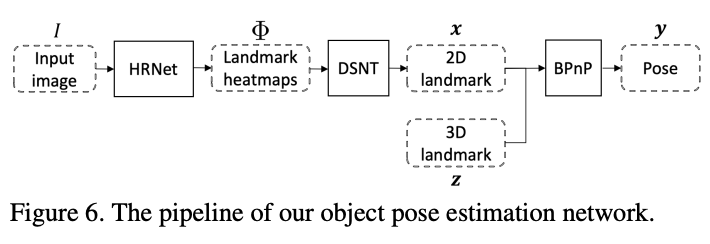
这一部分是描述一个已知地图 z 和相机内参 K ，根据观测的关键点坐标 x ，估计姿态 y 的过程，流程如下：

其 loss 用公式来描述：

\(l(\boldsymbol{x}, \boldsymbol{y})=\left\|\pi(\boldsymbol{z} \mid \boldsymbol{y}, \mathbf{K})-\pi\left(\boldsymbol{z} \mid \boldsymbol{y}^{*}, \mathbf{K}\right)\right\|_{2}^{2}+\lambda R(\boldsymbol{x}, \boldsymbol{y})\tag{13}\)

上述流程中一个重要更新梯度计算如下：

\(\frac{\partial \ell}{\partial \boldsymbol{\theta}}=\frac{\partial l}{\partial \boldsymbol{y}} \frac{\partial g}{\partial \boldsymbol{x}} \frac{\partial h}{\partial \boldsymbol{\theta}}+\frac{\partial l}{\partial \boldsymbol{x}} \frac{\partial h}{\partial \boldsymbol{\theta}}\tag{14}\)

下图演示了两种情况下的收敛过程，其中第一行都是 \(\lambda = 1\) 第二行都是 \(\lambda = 0\)。

Figure 1 代表 \(h(I; \theta) = \theta\)

Figure 2 代表一个修改的 VGG11 网络

从这两个实验中，我们可以看到不论是否使用正则项，二者均可收敛，在 \(\lambda = 1\) 时二者均可以达到更好的收敛效果。

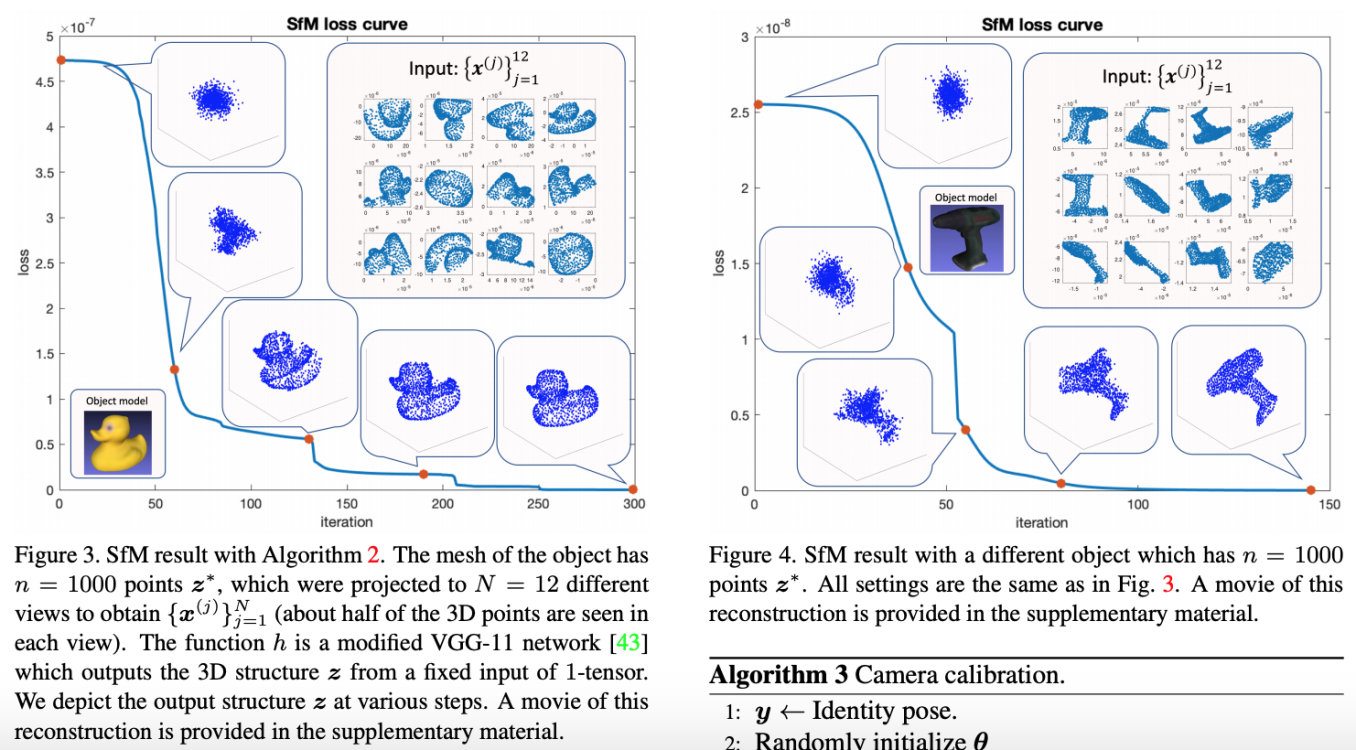
2.2 SfM with calibrated cameras

这一部分是

其中的 loss 定义如下：

\(l\left(\left\{\boldsymbol{y}^{(j)}\right\}_{j=1}^{N}, \boldsymbol{z}\right)=\sum_{j=1}^{N}\left\|\boldsymbol{x}^{(j)}-\pi\left(\boldsymbol{z}^{(j)} \mid \boldsymbol{y}^{(j)}, \mathbf{K}\right)\right\|_{2}^{2}\tag{15}\)
其中流程中的梯度推导如下：

\(\frac{\partial \ell}{\partial \boldsymbol{\theta}}=\sum_{j=1}^{N}\left(\frac{\partial l}{\partial \boldsymbol{z}^{(j)}} \frac{\partial \boldsymbol{z}^{(j)}}{\partial \boldsymbol{\theta}}+\frac{\partial l}{\partial \boldsymbol{y}^{(j)}} \frac{\partial \boldsymbol{y}^{(j)}}{\partial \boldsymbol{z}^{(j)}} \frac{\partial \boldsymbol{z}^{(j)}}{\partial \boldsymbol{\theta}}\right)\tag{16}\)
下图演示了一个 SfM 的收敛过程：

2.3 Camera calibration

相机标定流程如下：

其中 loss 定义如下：

\(l(\mathbf{K}, \boldsymbol{y})=\|\boldsymbol{x}-\pi(\boldsymbol{z} \mid \boldsymbol{y}, \mathbf{K})\|_{2}^{2}\tag{17}\)
梯度推导如下：

\(\frac{\partial \ell}{\partial \boldsymbol{\theta}}=\frac{\partial l}{\partial \mathbf{K}} \frac{\partial \mathbf{K}}{\partial \boldsymbol{\theta}}+\frac{\partial l}{\partial \boldsymbol{y}} \frac{\partial g}{\partial \mathbf{K}} \frac{\partial \mathbf{K}}{\partial \boldsymbol{\theta}}\tag{18}\)

3 Object pose estimation with BPnP

最终作者设计了一个基于 BPnP 的物体姿态估计流程：

论文&源码

论文：https://arxiv.org/abs/1909.06043
源码：https://github.com/BoChenYS/BPnP
Video：https://www.youtube.com/watch?v=eYmoAAsiBEE