NeRF является Oral докладом на ECCV 2020 и оказал огромное влияние, можно сказать, что он с нуля создал новый подход к реконструкции сцен на основе неявного представления с использованием нейронных сетей. Благодаря своей простой идее и отличным результатам, до сих пор существует множество связанных с 3D работ, основанных на этом методе.
Задача, которую решает NeRF, называется Novel View Synthesis (синтез новых ракурсов), то есть создание изображений сцены с любого нового ракурса на основе наблюдений с нескольких известных ракурсов (внутренние и внешние параметры камеры, изображения, позы и т.д.). В традиционных методах эта задача обычно решается с помощью трехмерной реконструкции и последующего рендеринга, однако NeRF стремится избежать явной трехмерной реконструкции и напрямую получать изображения с новых ракурсов, основываясь только на внутренних и внешних параметрах. Для достижения этой цели NeRF использует нейронную сеть как неявное представление 3D-сцены, заменяя традиционные методы, такие как облака точек, сетки, воксели, TSDF и т.д., что позволяет напрямую рендерить проекционные изображения с любого угла и позиции.

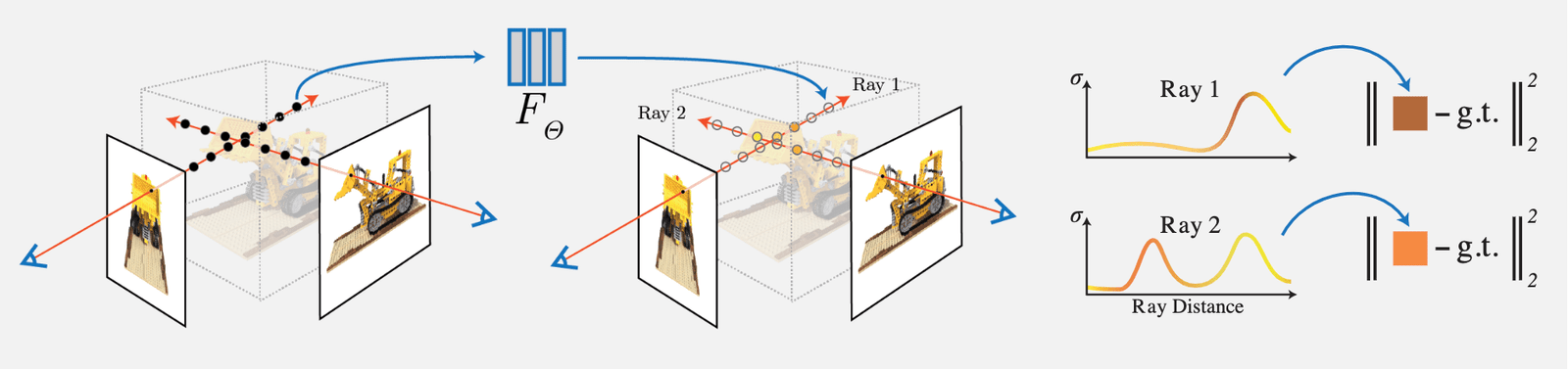
Идея NeRF довольно проста: с помощью воксельного рендеринга интегрировать плотность (непрозрачность) вдоль луча каждого пикселя изображения с входного ракурса, а затем сравнить полученное RGB-значение с истинным значением для расчета Loss. Поскольку воксельный рендеринг, описанный в статье, полностью дифференцируем, сеть может обучаться:

Основные задачи и нововведения следующие:
1) Предложен метод представления сложных геометрических и материальных непрерывных сцен с помощью 5D нейронного радиационного поля (Neural Radiance Field), параметризованного с использованием MLP сети.
2) Предложен улучшенный дифференцируемый метод рендеринга на основе классического воксельного рендеринга (Volume Rendering), который позволяет получать RGB-изображения через дифференцируемый рендеринг и использовать их как цель для оптимизации. Этот метод включает стратегию ускорения с использованием иерархической выборки, чтобы распределить емкость MLP на видимые области сцены.
3) Предложен метод позиционного кодирования (Position Encoding), который отображает каждую 5D координату в пространство более высокой размерности, что позволяет лучше выражать высокочастотные детали в нейронном радиационном поле.

1 Представление сцены с помощью нейронного радиационного поля (Neural Radiance Field Scene Representation)

NeRF представляет непрерывную сцену как 5D вектор-функцию, где:

• Входные данные: 3D позиция \mathbf{x}=(x, y, z) и 2D направление ракурса (\theta, \phi)
• Выходные данные: цвет излучения \mathbf{c}=(r, g, b) и объемная плотность (непрозрачность) \sigma.

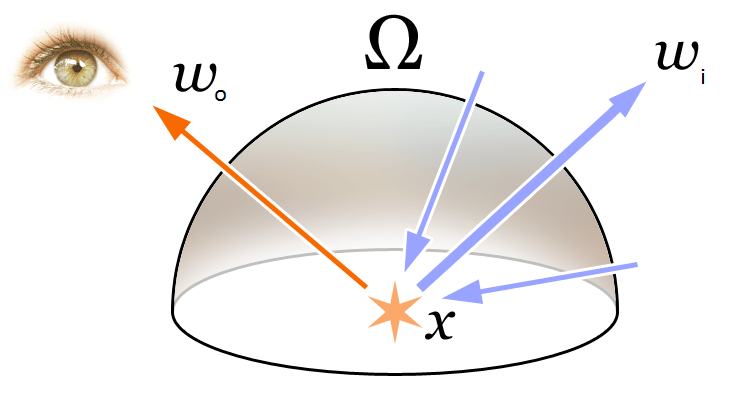
Для интуитивного объяснения 2D направления ракурса можно использовать следующую диаграмму:

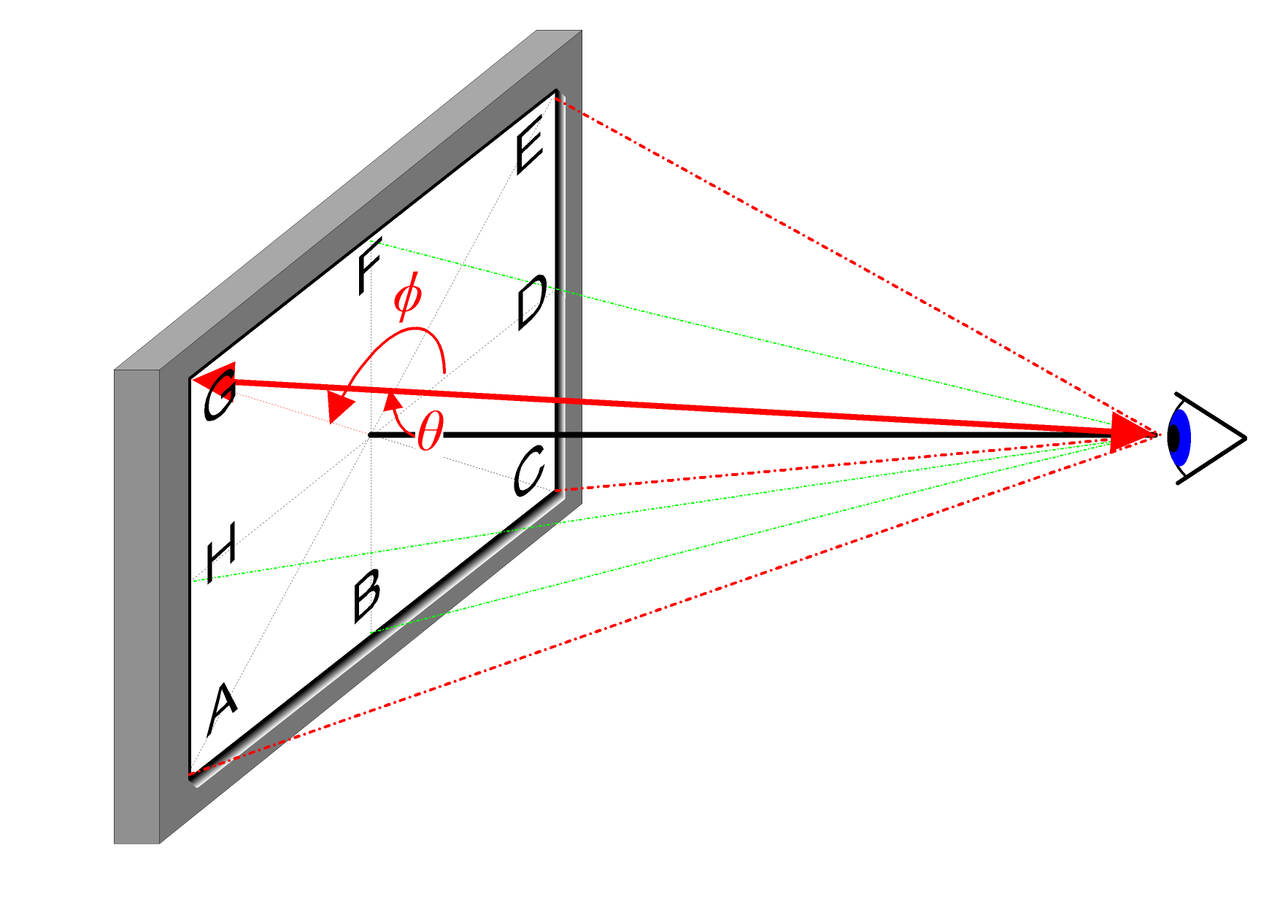
В реальной реализации направление ракурса представляется как единичный вектор в трехмерной декартовой системе координат \mathbf{d}, то есть линия, соединяющая любую точку изображения с центром камеры. Мы используем полносвязную сеть MLP для представления этого отображения:
\begin{equation}F_{\Theta}:(\mathbf{x}, \mathbf{d}) \rightarrow(\mathbf{c}, \sigma)\end{equation}

Обучение этого отображения осуществляется путем оптимизации параметров сети \Theta, чтобы получить соответствие между 5D координатами на входе и цветом и плотностью на выходе.

Чтобы сеть могла обучиться представлению с разных ракурсов, мы делаем два разумных предположения:

• Объемная плотность (непрозрачность) \sigma зависит только от 3D позиции \mathbf{x} и не зависит от направления ракурса \mathbf{d}. Плотность объекта в разных точках не должна зависеть от угла обзора, что очевидно.
• Цвет \mathbf{c} зависит как от 3D позиции \mathbf{x}, так и от направления ракурса \mathbf{d}.

Часть сети, предсказывающая объемную плотность \sigma, получает на вход только позицию \mathbf{x}, а часть, предсказывающая цвет \mathbf{c}, получает на вход как позицию, так и направление \mathbf{d}. В конкретной реализации:

• MLP сеть F_{\Theta} сначала обрабатывает 3D координаты \mathbf{x} через 8 слоев полносвязных слоев (с функцией активации ReLU, по 256 каналов в каждом слое), чтобы получить \sigma и 256-мерный вектор признаков.
• Этот 256-мерный вектор признаков объединяется с направлением ракурса \mathbf{d} и подается на другой полносвязный слой (с функцией активации ReLU, по 128 каналов в каждом слое), который на выходе предсказывает RGB цвет, зависящий от направления.

Пример структуры сети, предложенной в статье, выглядит следующим образом:

На рисунке 3 показано, что наша сеть может моделировать неламбертовские эффекты (non-Lambertian effects); на рисунке 4 показано, что если при обучении не учитывать зависимость от ракурса (View Dependence) (только \mathbf{x}), то сеть не сможет моделировать блики.

2 Воксельный рендеринг с использованием радиационных полей (Volume Rendering with Radiance Fields)

2.1 Классическое уравнение рендеринга

Чтобы понять концепции Volume Rendering и Radiance Field, рассмотренные в статье, сначала вспомним основное уравнение рендеринга в компьютерной графике:
\begin{equation}\begin{array}{l}L_{o}(\boldsymbol{x}, \boldsymbol{d}) &=L_{e}(\boldsymbol{x}, \boldsymbol{d})+\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \left(\boldsymbol{\omega}_{i}, \boldsymbol{n}\right) d \boldsymbol{\omega}_{i}\\&=L_{e}(\boldsymbol{x}, \boldsymbol{d})+\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \cos \theta d \boldsymbol{\omega}_{i}\end{array}\end{equation}

Как показано на рисунке выше, уравнение рендеринга описывает излучение (исходящий свет) L_{o}(\boldsymbol{x}, \boldsymbol{d}) в направлении \mathbf{d} из 3D позиции \mathbf{x}. Это излучение состоит из собственного излучения точки L_{e}(\boldsymbol{x}, \boldsymbol{d}) и отраженного излучения от внешних источников. В частности:

• L_{e}(\boldsymbol{x}, \boldsymbol{d}) — это излучение, испускаемое точкой \mathbf{x} в направлении \mathbf{d}, если точка является источником света.
• \int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \cos \theta d \boldsymbol{\omega}_{i} — это интеграл по полусфере направлений падения света.
• f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) — это функция рассеяния, которая описывает долю света, отраженного от точки в направлении \mathbf{d} из направления \boldsymbol{\omega}_{i}.
• L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) — это излучение, приходящее в точку \mathbf{x} из направления \boldsymbol{\omega}_{i}.
• \boldsymbol{n} — это нормаль в точке \mathbf{x}, а \theta — угол между направлением \boldsymbol{\omega}_{i} и нормалью \boldsymbol{n}, так что \left(\boldsymbol{\omega}_{i}, \boldsymbol{n}\right)=\cos \theta.

Простое понимание концепции излучения заключается в том, что свет — это электромагнитное излучение. Мы знаем, что длина волны \lambda и частота \nu электромагнитной волны связаны следующим уравнением:
\begin{equation}c=\lambda \nu\end{equation}

Иными словами, их произведение равно скорости света c. Мы также знаем, что цвета видимого света (RGB) — это результат воздействия излучения с различными частотами на камеру. Таким образом, в NeRF радиационное поле рассматривается как приближенное моделирование цвета.

2.2 Классический метод воксельного рендеринга

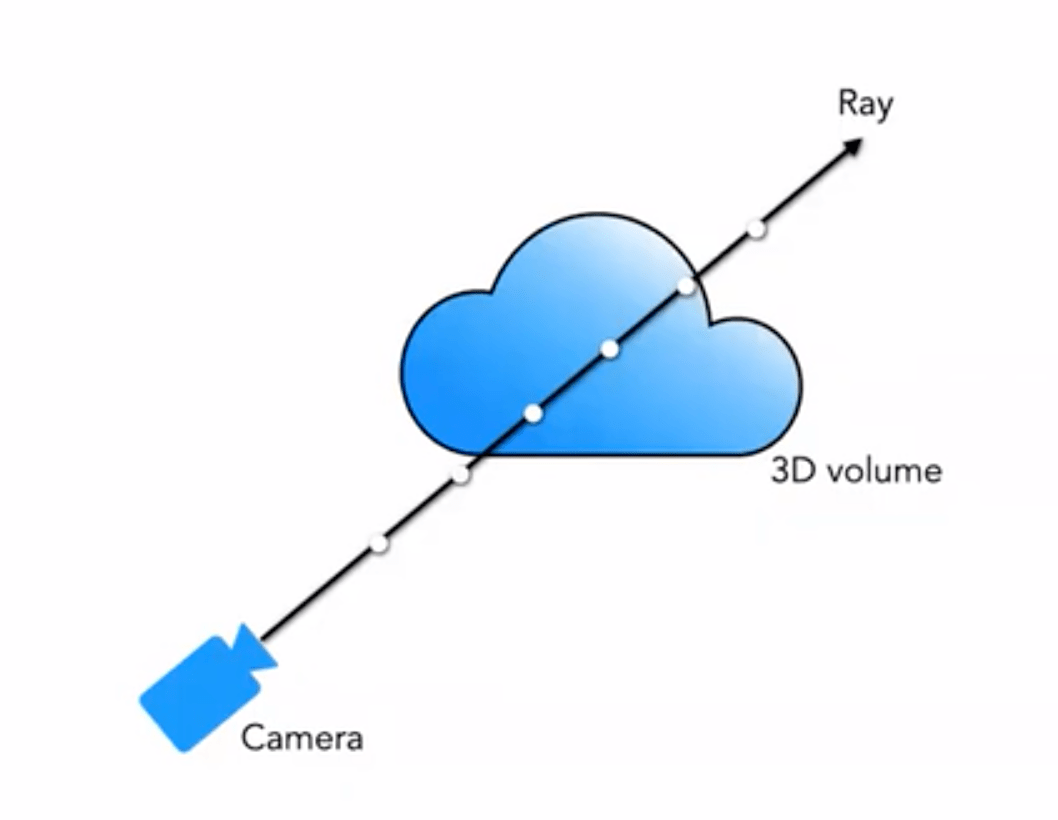
Часто мы сталкиваемся с рендерингом сеток, вокселей и т.д. Для многих эффектов, таких как облака, дым и т.п., часто используется воксельный рендеринг:

Наше 5D нейронное радиационное поле представляет сцену как воксельную плотность и направленную радиационную яркость в любой точке пространства. Воксельная плотность \sigma(\mathbf{x}) определяется как вероятность того, что луч остановится в точке \mathbf{x} (или, другими словами, вероятность того, что луч прекратит свое движение после прохождения через эту точку). Используя принципы классического объемного рендеринга, мы можем рендерить цвет луча, проходящего через сцену.

Таким образом, для луча, исходящего из ракурса \mathbf{o} в направлении \mathbf{d}, точка, в которую он попадает в момент времени t, будет:
\begin{equation}\mathbf{r}(t)=\mathbf{o}+t \mathbf{d}\end{equation}
Тогда интегрируя цвет вдоль этого направления в пределах диапазона (t_n, t_f), мы получаем итоговое значение цвета C(\mathbf{r}):

Функция T(t) описывает накопленную прозрачность луча от t_n до t. Иными словами, это вероятность того, что луч пройдет от t_n до t, не встретив никаких частиц. С помощью этого определения рендеринг изображения можно выразить как интеграл для C(\mathbf{r}), который представляет собой цвет, полученный лучом камеры, проходящим через каждый пиксель.

Функция \sigma(\mathbf{x}) (Объемная плотность \sigma(\mathbf{x}) может интерпретироваться как дифференциальная вероятность того, что луч прекратит свое движение в бесконечно малой частице в точке \mathbf{x}.)

2.3 Воксельный рендеринг на основе сегментированной выборки

Однако в реальном рендеринге мы не можем выполнять непрерывное интегрирование, поэтому используем метод численного интегрирования (квадратурный метод). Мы делим диапазон \left[t_{n}, t_{f}\right] на равномерно распределенные сегменты с помощью стратифицированной выборки (stratified sampling) и выполняем равномерную выборку в каждом сегменте. Способ деления следующий:
\begin{equation}t_{i} \sim \mathcal{У}\left[t_{n}+\frac{i-1}{N}\left(t_{f}-t_{n}\right), t_{n}+\frac{i}{N}\left(t_{f}-t_{n}\right)\right]\end{equation}

Для выборки используем метод дискретного интегрирования:
\begin{equation}\hat{C}(\mathbf{r})=\sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}, \text { где } T_{i}=\exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right)\end{equation}
где \delta_{i}=t_{i+1}-t_{i} — это расстояние между соседними выборками.

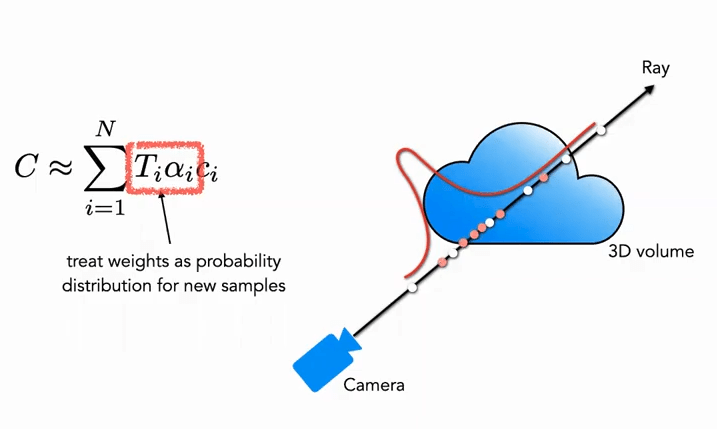
Ниже показан процесс воксельного рендеринга:

3 Оптимизация нейронного радиационного поля (Optimizing a Neural Radiance Field)

Описанный выше метод является основой NeRF, но полученные результаты не всегда оптимальны, например, могут наблюдаться недостаточная детализация или медленная скорость обучения. Чтобы улучшить точность реконструкции и ускорить процесс обучения, мы вводим следующие две стратегии:

• Positional Encoding (позиционное кодирование): эта стратегия позволяет MLP лучше представлять высокочастотную информацию, что приводит к более детализированным результатам;
• Hierarchical Sampling Procedure (иерархическая процедура выборки): эта стратегия позволяет более эффективно выбирать высокочастотную информацию во время обучения.

3.1 Positional Encoding (позиционное кодирование)

Хотя теоретически нейронные сети могут аппроксимировать любую функцию, эксперименты показали, что MLP, обрабатывающая входные данные (x, y, z, \theta, \phi), не может полностью выразить детали. Это соответствует выводам работы Рахамана и др. («On the spectral bias of neural networks. In: ICML (2018)»), которые доказали, что нейронные сети склонны обучаться низкочастотным функциям. Они также показали, что отображение входных данных в пространство более высокой размерности с помощью высокочастотных функций позволяет лучше аппроксимировать высокочастотную информацию в данных.

Применяя эти выводы к задаче представления сцены с помощью нейронных сетей, мы модифицируем F_{\Theta} как комбинацию двух функций: F_{\Theta}=F_{\Theta}^{\prime} \circ \gamma, что значительно улучшает способность сети выражать детали. В этом случае:

• \gamma — это функция кодирования, отображающая из \mathbb{R} в пространство более высокой размерности \mathbb{R}^{2 L};
• F_{\Theta}^{\prime} — это обычная MLP сеть.

Используемая в статье функция кодирования выглядит следующим образом:

Функция \gamma(\cdot) применяется к трехмерным координатам положения \mathbf{x} (нормализованным до [-1, 1]) и декартовым координатам направления взгляда \mathbf{d}. В этой статье для \gamma(\mathbf{x}) установлено L=10; для \gamma(\mathbf{d}) установлено L=4.

Таким образом, длина кодирования для трехмерных координат положения равна: 3 \times 2 \times 10 = 60, а для кодирования положения направления взгляда — 3 \times 2 \times 4 = 24, что соответствует входным размерам на схеме сети.

Аналогично, в Transformer также есть операция позиционного кодирования, но она принципиально отличается от той, что используется в этой статье. В Transformer позиционное кодирование используется для представления последовательной информации входных данных, тогда как здесь позиционное кодирование применяется для отображения входных данных в высокие измерения, что позволяет сети лучше обучаться извлекать высокочастотную информацию.

3.2 Hierarchical Sampling Procedure (Иерархическая процедура выборки)

Иерархическая процедура выборки основана на ускорении классических алгоритмов рендеринга. В описанном выше методе объемного рендеринга (Volume Rendering) выборка точек на луче влияет на итоговую эффективность: если точек слишком много, вычисления становятся слишком медленными, а если слишком мало, то приближение становится неточным. Естественным решением является более плотная выборка вблизи точек с большим вкладом в цвет и более редкая выборка вблизи точек с меньшим вкладом. На основе этой идеи NeRF предложил иерархическую процедуру выборки от грубой к детализированной (Coarse to Fine).

Часть Coarse: Сначала для грубой сети мы выбираем N_c редких точек (c обозначает Coarse) и модифицируем уравнение (3) в новой форме (с добавлением весов):
\begin{equation}\hat{C}_{c}(\mathbf{r})=\sum_{i=1}^{N_{c}} w_{i} c_{i}, \quad w_{i}=T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right)\end{equation}
Где веса должны быть нормализованы:
\begin{equation}\hat{w}_{i}=\frac{w_{i}}{\sum_{j=1}^{N_{c}} w_{j}}\end{equation}

Эти веса \hat{w}_{i} можно рассматривать как кусочно-постоянную функцию плотности вероятности вдоль луча (Piecewise-constant PDF). С помощью этой функции плотности вероятности можно приблизительно определить распределение объектов вдоль луча.

Часть Fine: На втором этапе мы используем выборку методом обратного преобразования (Inverse Transform Sampling), чтобы на основе полученного распределения выбрать второй набор точек N_f. В итоге мы снова используем уравнение (3) для вычисления \hat{C}_{f}(\mathbf{r}). Однако на этот раз используются все N_c + N_f образцов. Этот метод позволяет второй выборке сосредоточиться на областях с реальным содержанием сцены, реализуя важностную выборку (Importance Sampling).

Как показано на рисунке, белые точки представляют собой точки первой равномерной выборки, после которой получено распределение. Вторая выборка (красные точки) проводится на основе этого распределения: в областях с высокой вероятностью выборка плотнее, а в областях с низкой вероятностью — реже (очень похоже на фильтрацию частиц).

3.3 Implementation Details (Детали реализации)

Что касается функции потерь при обучении, то определение здесь очень простое и прямолинейное: для грубой и детализированной сетей используется L_2 Loss рендеринга, который выражается следующим образом:
\begin{equation}\mathcal{L}=\sum_{\mathbf{r} \in \mathcal{R}}\left[\left\|\hat{C}_{c}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}+\left\|\hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}\right]\end{equation}

Где:

• \mathcal{R} обозначает набор всех лучей, выбранных в одном батче
• C(\mathbf{r}) обозначает истинный RGB-цвет
• \hat{C}_{c}(\mathbf{r}) обозначает предсказанный грубой сетью RGB-цвет
• \hat{C}_{f}(\mathbf{r}) обозначает предсказанный детализированной сетью RGB-цвет

4 Results (Результаты экспериментов)

В статье сравниваются результаты с рядом других работ, таких как:

• Neural Volumes (NV): https://github.com/facebookresearch/neuralvolumes
• Scene Representation Networks (SRN): https://github.com/vsitzmann/scene-representation-networks
• Local Light Field Fusion (LLFF): https://github.com/Fyusion/LLFF

4.1 Datasets (Наборы данных)

Авторы сравнили результаты на различных наборах данных, и можно увидеть, что на большинстве из них метод значительно превосходит другие:

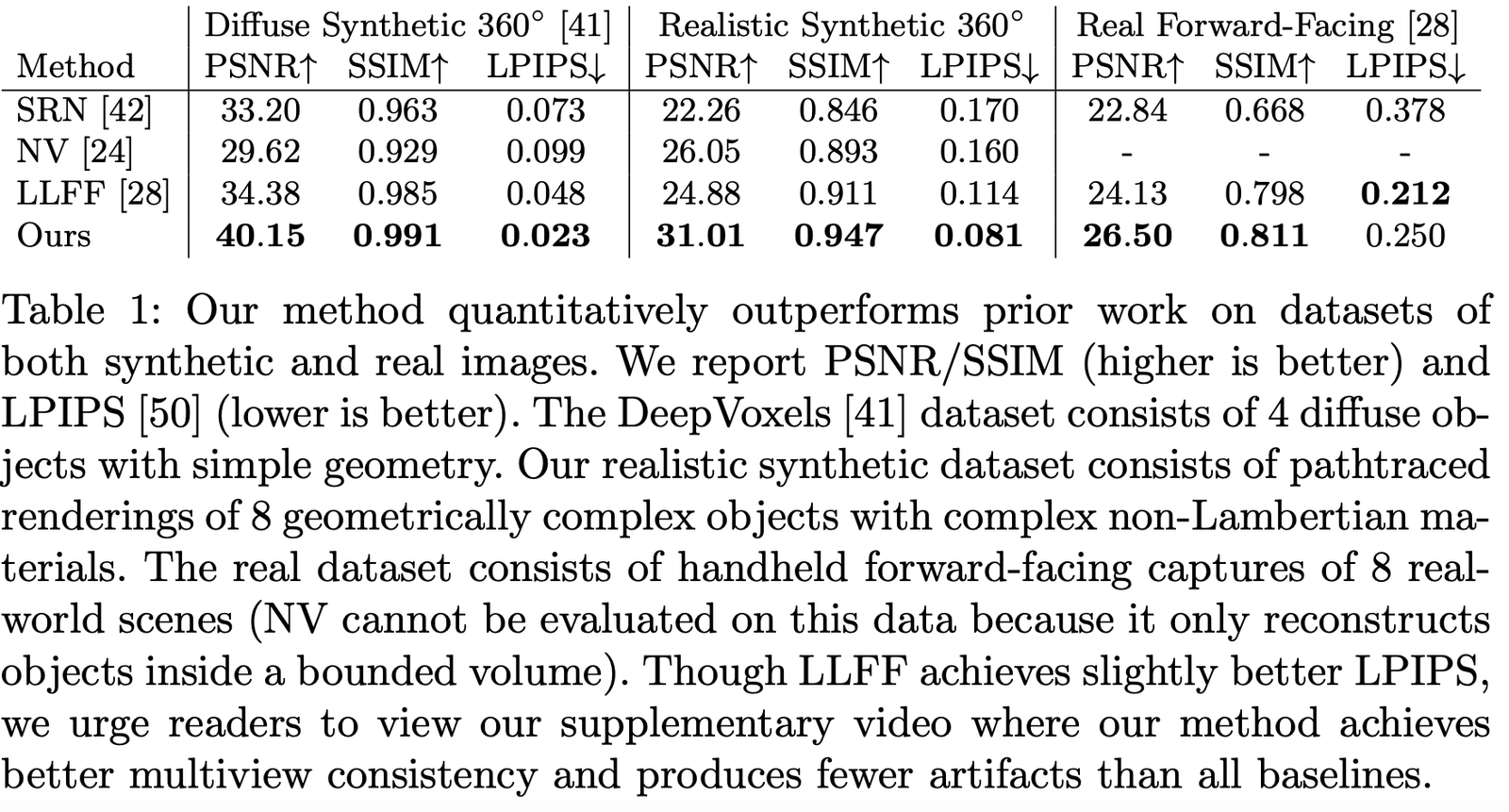
Визуализация на симулированных наборах данных:

Визуализация на реальных наборах данных:

4.2 Ablation Studies (Исследования методом исключения)

Мы провели исследования методом исключения на наборе данных Realistic Synthetic 360◦ при различных параметрах и настройках, результаты приведены ниже:

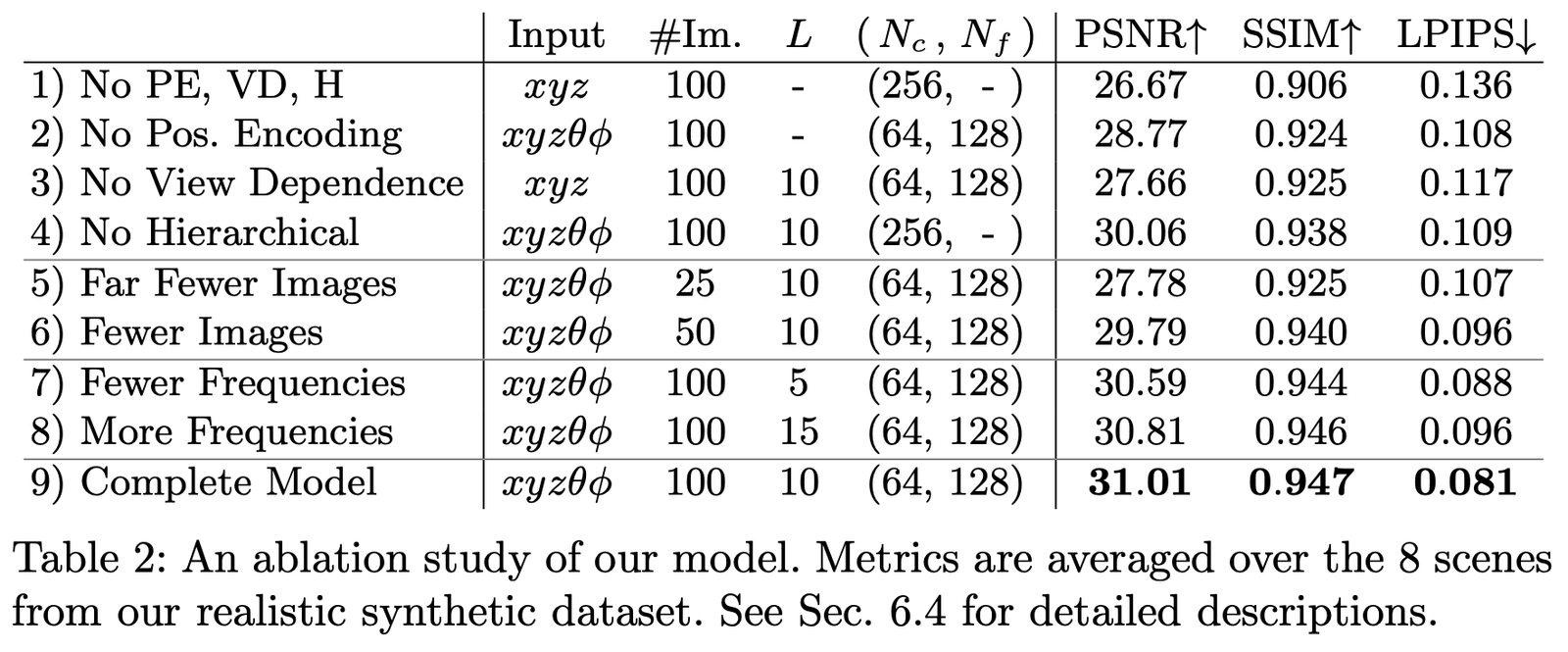
Основные сравниваемые настройки:

• Позиционное кодирование (PE), т.е. \mathbf{x}
• Зависимость от вида (VD), т.е. \mathbf{d}
• Иерархическая выборка (H)

Где:
1-я строка представляет минимальную сеть без каких-либо из этих компонентов;
2-4 строки представляют сети, в которых поочередно исключается один из компонентов;
5-6 строки показывают различия при уменьшении количества изображений для выборки;
7-8 строки показывают различия при изменении частоты L (уровень разложения частоты позиционного кодирования \mathbf{x}).

Заключение статьи

Главное нововведение этой статьи заключается в том, что с помощью неявного представления удалось обойти необходимость ручного проектирования методов представления трехмерных сцен, что позволяет обучаться трехмерной информации сцены на более высоком уровне. Однако недостатком является очень медленная скорость, что было улучшено в последующих работах. С другой стороны, интерпретируемость и возможности неявного представления все еще требуют дальнейших исследований.
Тем не менее, можно с уверенностью сказать, что такой простой и эффективный подход в будущем станет революцией в реконструкции 3D и 4D сцен и приведет к новому прорыву в области трехмерного зрения.

Скачать статью

PDF | Вебсайт | Код (официальный) | Код (Pytorch Lightning) | Запись | Запись (Bilibili)
Пример Colab: Tiny NeRF | Full NeRF

Ссылки на материалы

[1] Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis[C]//European Conference on Computer Vision. Springer, Cham, 2020: 405-421.
[2] https://www.cnblogs.com/noluye/p/14547115.html
[3] https://www.cnblogs.com/noluye/p/14718570.html
[4] https://github.com/yenchenlin/awesome-NeRF
[5] https://zhuanlan.zhihu.com/p/360365941
[6] https://zhuanlan.zhihu.com/p/380015071
[7] https://blog.csdn.net/ftimes/article/details/105890744
[8] https://zhuanlan.zhihu.com/p/384946242
[9] https://zhuanlan.zhihu.com/p/386127288
[10] https://blog.csdn.net/g11d111/article/details/118959540
[11] https://www.bilibili.com/video/BV1fL4y1T7Ag
[12] https://zh.wikipedia.org/wiki/%E6%B8%B2%E6%9F%93%E6%96%B9%E7%A8%8B
[13] https://zhuanlan.zhihu.com/p/380015071
[14] https://blog.csdn.net/soaring_casia/article/details/117664146
[15] https://www.youtube.com/watch?v=Al6NTbgka1o
[16] https://github.com/matajoh/fourier_feature_nets

Связанные работы

DSNeRF: https://github.com/dunbar12138/DSNeRF (SfM ускоряет NerF)
BARF: https://github.com/chenhsuanlin/bundle-adjusting-NeRF
PlenOctrees: https://alexyu.net/plenoctrees/ (ускорение рендеринга NeRF с помощью PlenOctrees)
https://github.com/google-research/google-research/tree/master/jaxnerf (ускорение обучения с использованием JAX)