截断符号距离 | TSDF, Truncated Signed Distance Function

1 定义

TSDF（Truncated Signed Distance Function）是截断符号距离函数的缩写，各个体素的截断符号距离组成了 TSDF 场。理解 TSDF 首先要理解下符号距离 SDF。如下图所示：

假设相机光心到表面的距离为 d_s，到射线上体素 \vec x 距离为 d_v，则符号距离就是 SDF(x) = d_{\vec x}。
显然，当 d_{\vec x} \gt 0 时，表示体素在平面前方，当d_{\vec x} \lt 0 时，表示体素在平面后方。

体素的概率值是我们更新体素距离的方式。因为体素距离平面过远时，其数值对于平面影响过小因此通常都会采用 TSDF 设定一个阈值 \delta 来截断，类似下图：

用公式定义如下：
\begin{equation}\operatorname{TSDF}(x) =\begin{cases}1 & \text{ if } x \gt \delta \\\frac{\operatorname{SDF}(x)}{\left | \delta \right | } & \text{ if } -\delta \le x \le \delta \\-1 & \text{ if } x \lt \delta\end{cases}\end{equation}

如果是在 2D 平面上，一个简单的 TSDF 场类似下面的样子：

2 融合

2.1 权重

有了上述 TSDF 的定义，想要对于多个不同帧的同一个体素观测进行更新，首先要定义体素的概率，考虑到一个显然的事实，对于一个深度传感器来说，测量数据的方差与角度有关：

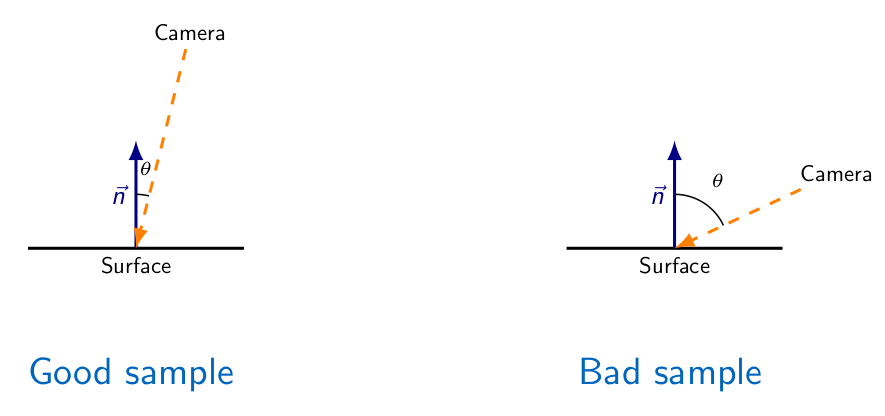
则可以想到一种基本的权重定义如下：
\begin{equation}w(p) = \frac{\operatorname{cos}(\theta)}{\operatorname{distance}(v)}\end{equation}
其中 \operatorname{distance}(v)=d_v。

2.2 更新

对于同一个体素多次不同观测，我们采用如下方式更新：
1）初始化：
\begin{equation}\left\{\begin{matrix}T S D F_{0}(\mathbf{x})=0 \\W_{0}(\mathbf{x})=0\end{matrix}\right.\end{equation}

2）更新 TSDF 和 W 值：
\begin{equation}\begin{aligned}T S D F_{i}(\mathbf{x}) &=\frac{W_{i-1}(\mathbf{x}) T S D F_{i-1}(\mathbf{x})+w_{i}(\mathbf{x}) t s d f_{i}(\mathbf{x})}{W_{i-1}(\mathbf{x})+w_{i}(\mathbf{x})} \\W_{i}(\mathbf{x}) &=W_{i-1}(\mathbf{x})+w_{i}(\mathbf{x})\end{aligned}\end{equation}
其中小写 tsdf 和 w 表示更新之前的观测值（对于相机视野外的情况 w=0 对于是业内的情况 w=1），大写 TSDF 和 W 表示更新之后的值。反复执行上述操作即可将新的帧融合到之前的帧上。

参考文献

[1] https://wlsdzyzl.top/2019/01/25/3D-Reconstruction%E2%80%94%E2%80%94TSDF-volume-reconstruction/
[2] https://www.jianshu.com/p/462fe75753f7
[3] Truncated Signed Distance Function: Experiments on Voxel Size