论文笔记:UnsuperPoint: End-to-end Unsupervised Interest Point Detector and Descriptor
SuperPoint 的工作取得了巨大的成功,但是有一个非常明显的问题就是训练和真值获取非常困难(采用仿真辅助)。在实际场景中,想要进行人工标注再 finetune 是比较难的。因此本文提出了一种无监督学习的方式同时获得关键点与描述子,虽然无监督,但是在数据集上取得了很好效果的同时也达到了很快的速度。
1 网络设计
本文的网络设计大体与 SuperPoint 一致,但是在 head 设计上面有很多细节不同,主要是 SuperPoint 主要使用分类方式离散地定位关键点坐标、是否为关键点等信息。在 UnsuperPoint 中,作者使用了 score map 作为关键点置信度指标、使用回归 offset 方式进行关键点定位。它的网络设计如下:
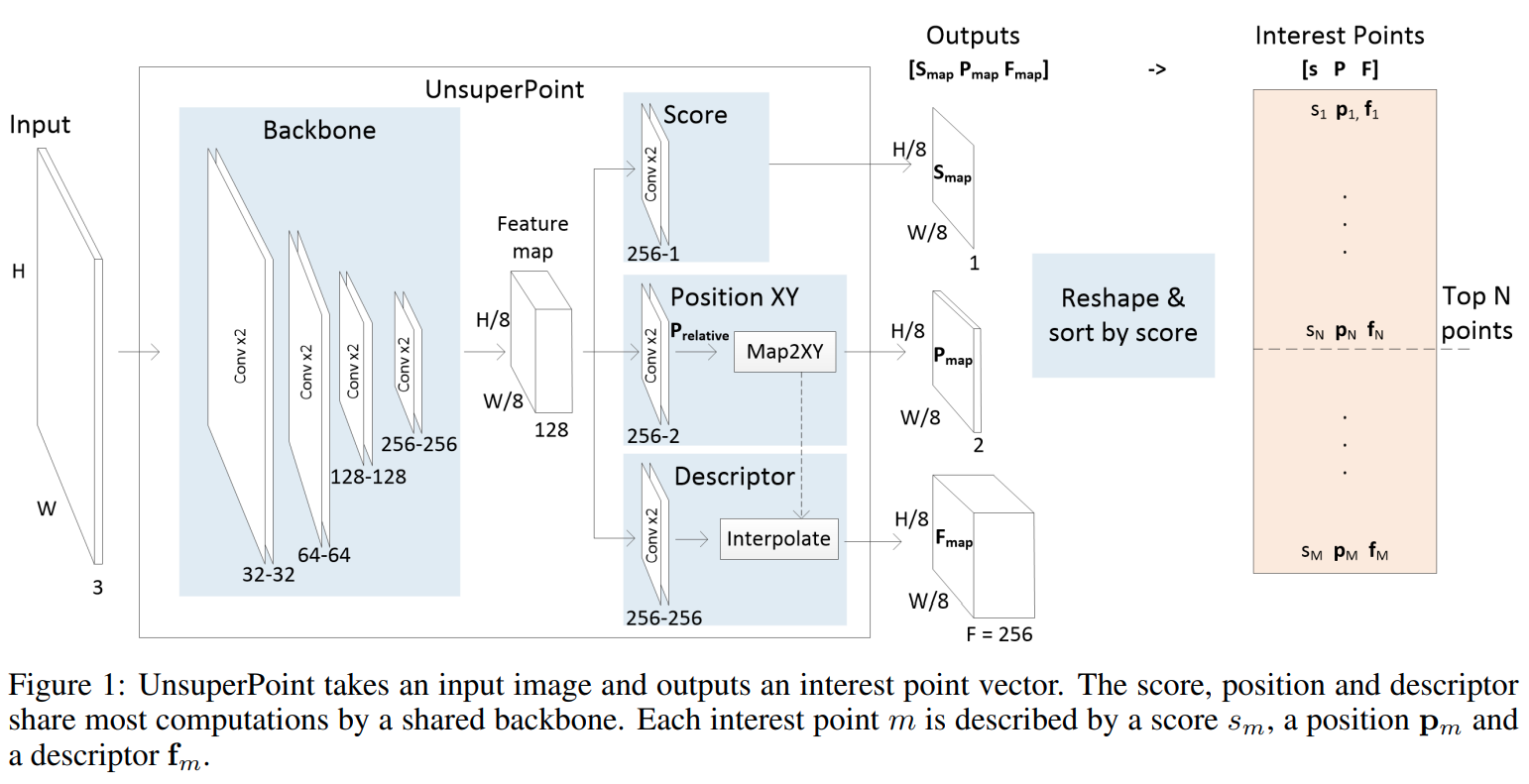
1.1 Backbone Module
本文的 Backbone module 与 SuperPoint 类似是一个 FCN 的网络结构,每一层都是两个 conv + maxpooling,总共进行了3次下采样,通道数分别是:32-32-64-64-128-128-256-256。
那么在最终的 feature map 上一个点对应于原图中 8x8 大小的区域。
1.2 Score Module S_{map}
Score module S_{map} 通过回归的方式得到每个点是否为关键点的分数,或者说置信度([0-1]之间),它由 conv-256 + conv-1 构成,激活函数是 sigmoid。和传统方法一样,这一分数用来选择 top N 的关键点。
1.3 Position Module P_{map}
Position module 预测关键点的位置。与 SuperPoint 采用分类方式(64 channel 分别预测一个位置是否为关键点)不同,本文采用回归的方式预测一个 8x8 块内关键点的坐标偏移量 offset(归一化为 [0-1] 之间)。它的结构是 conv-256 + conv-2,激活函数是 sigmoid。如下图所示是一个 24x24 大小的图示意,对于进行了 8 倍下采样的 FCN 而言,position module 实际上预测了 3x3 = 9 的 keypoint 位置:
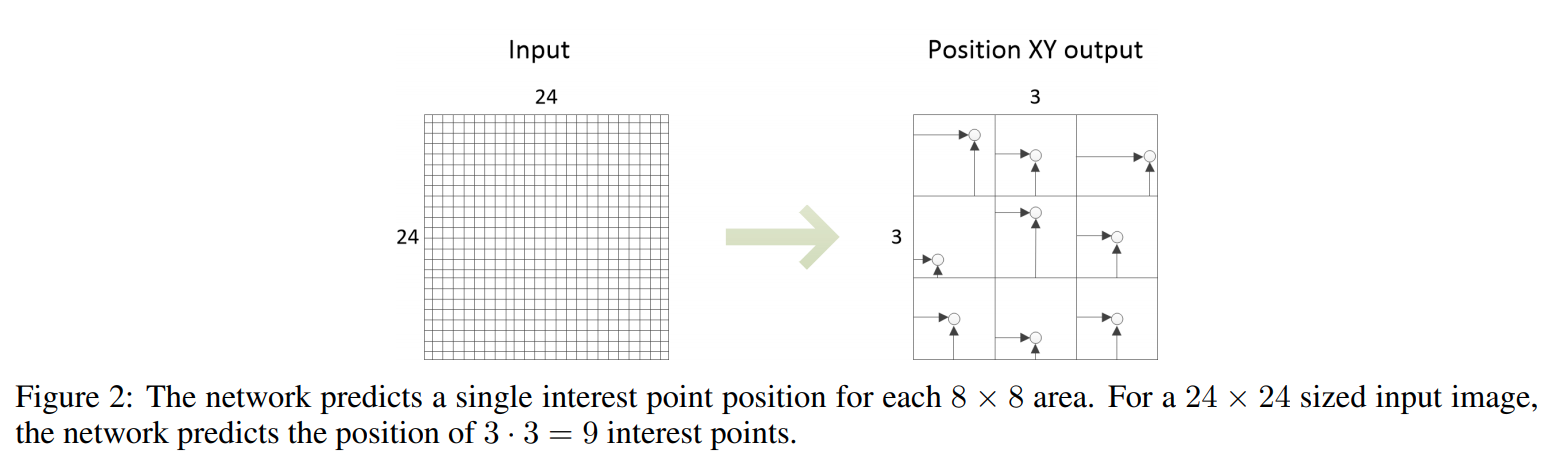
其中计算偏移量的公式如下:
\begin{array}{l}\mathbf{P}_{\operatorname{map}, \mathbf{x}}(r, c)=\left(c+\mathbf{P}_{\text {relative }, \mathbf{x}}(r, c)\right) \cdot f_{\text {downsample }} \\\mathbf{P}_{\text {map }, \mathbf{y}}(r, c)=\left(r+\mathbf{P}_{\text {relative,y }}(r, c)\right) \cdot f_{\text {downsample }}\tag{1}\end{array}本文中 f_{\text {downsample}} = 8。
1.4 Descriptor Module F_{map}
Descriptor module F_{map} 表示关键点的描述信息,用于区分每个关键点的匹配相似程度。它由 conv256 - conv256 组成,描述子大小为 256 floats。前一部分得到的是 256 channels 的feature map,代表每个 8x8 块的描述,后面这一 model 使用所有 P_{map} 中的关键点位置通过内插来重新得到每个关键点位置的描述子。正是由于上述的 P_{map} 采用回归方式获得关键点坐标,加上这里的差值方式,使得描述子获取过程变成一个可微的过程,这一部分在训练过程中会用到。
2 自监督框架
这一部分解释了如何进行自监督方式的训练。整体流程如下图所示:
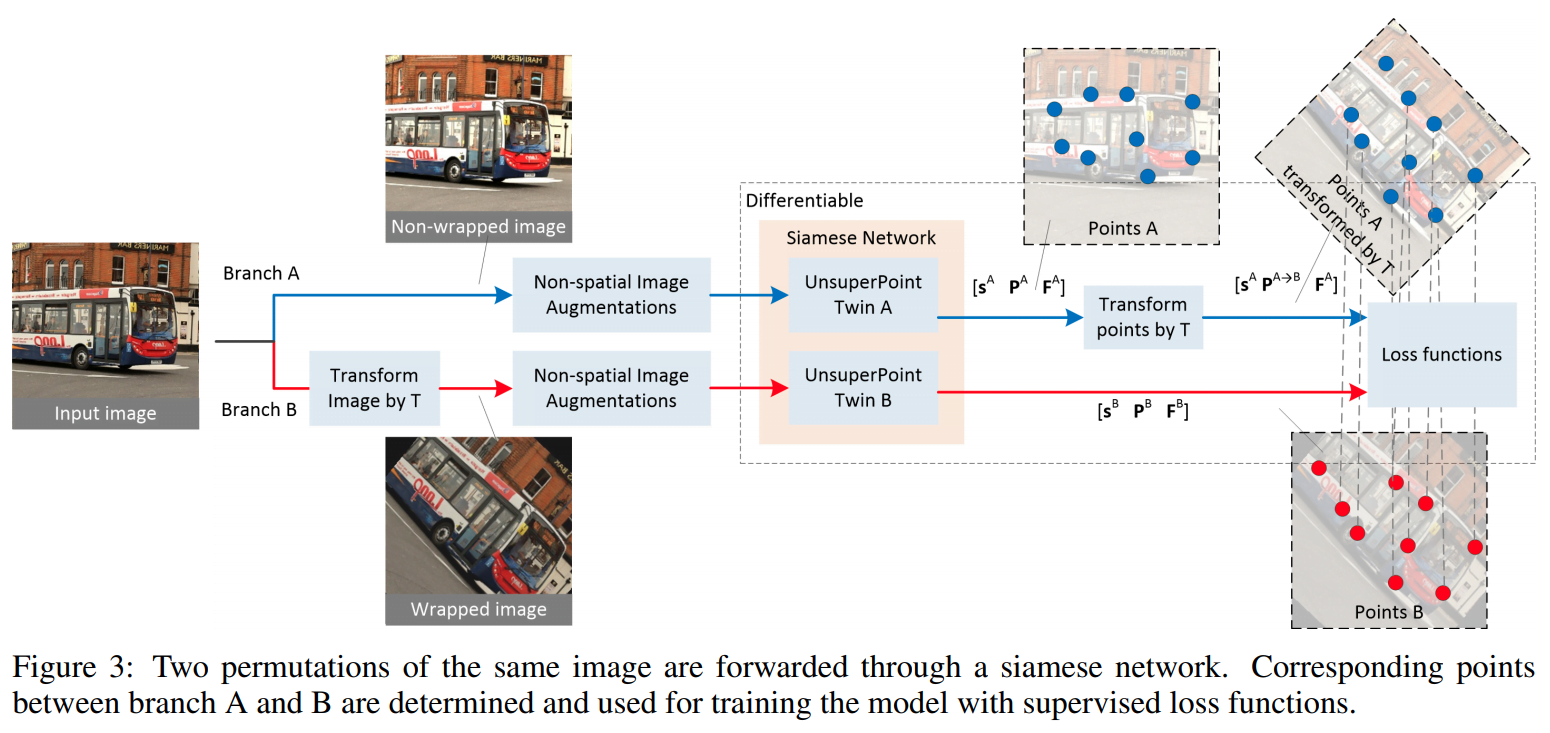 3
3
这一图示很显然,其实和监督的方式很像,就是利用图片进行 T 的 Transform,将原图进行变换,变换前后的图分别提取 score、point、feature 三个结果为 S^A、P^A 和 F^A,以及 S^B、P^B 和 F^B。对于其中点的位置进行 T 的 transform 变换到 P^B 位置,得到 Point-pair correspondences,利用匹配关系就得到了想要的无监督信号。
3 Loss functions
本文采用联合训练三个分支的方式,整体的 Loss 公式如下:
\begin{aligned}\mathcal{L}_{\text {total }}=& \alpha_{\text {usp }} \mathcal{L}^{\text {usp }} \\&+\alpha_{\text {uni\_xy }} \mathcal{L}^{\text {uni\_xy }} \\&+\alpha_{\text {desc }} \mathcal{L}^{\text {desc }}+\alpha_{\text {decorr }} \mathcal{L}^{\text {decorr }}\tag{2}\end{aligned}每一部分都加入了一个影响因子 \alpha。
Point-pair correspondences
对于两个图片提取的输出集合 b \in\{A, B\},其中每次输出3个 tensor \mathbf{s}^b、\mathbf{P}^b 和 \mathbf{F}^b。为了计算后文中的 Loss ,我们需要定义两张图片的匹配点对。设 \mathbf{M}^A 和 \mathbf{M}^B 分别定义了两张图片的 branch 输出,那么他们的距离就定义为 \mathbf{G} = \mathbf{M}^A \times \mathbf{M}^B。公式如下:
\mathbf{G}=\left[g_{i j}\right]_{M^{\mathrm{A}} \times M^{\mathrm{B}}}=\left[\left\|\mathbf{p}_{i}^{\mathrm{A} \rightarrow \mathrm{B}}-\mathbf{p}_{j}^{\mathrm{B}}\right\|_{2}\right]_{M^{\mathrm{A}} \times M^{\mathrm{B}}}\tag{3}其中 \mathbf{p}_{i}^{\mathrm{A} \rightarrow \mathrm{B}}=T \mathbf{p}_{i}^{\mathrm{A}}\tag{4}。
最近邻
如果 A 中的 point i 和 B 中的 point j 的距离 g_{ij} < \epsilon_{correspond},则称他们为最近邻。
有了这一定义后,我们对于 B 中给定的 tensor \mathbf{s}^b、\mathbf{P}^b 和 \mathbf{F}^b,我们可以找到 K 个最近邻,设为 \hat{\mathbf{s}^b} 、\hat{\mathbf{P}^b} 和 \hat{\mathbf{F}^b},其中每个点的下标为 k。则我们定义最近邻中第 k 个点 score 为 \hat{s_k^b}、position 为 \hat{\mathbf{p}_k^b} 以及 descriptor 为 \hat{\mathbf{f}_k^b}。当然他们的位置距离为:
d_{k}=\left\|T \hat{\mathbf{p}}_{k}^{\mathrm{A}}-\hat{\mathbf{p}}_{k}^{\mathrm{B}}\right\|=\left\|\hat{\mathbf{p}}_{k}^{\mathrm{A} \rightarrow \mathrm{B}}-\hat{\mathbf{p}}_{k}^{\mathrm{B}}\right\|\tag{5}3.1 Unsupervised point loss \mathcal{L}^{u s p}
这一 unsupervised point loss \mathcal{L}^{u s p} 定义如下:
\mathcal{L}^{u s p}=\alpha_{\text {position }} \sum_{k=1}^{K} l_{k}^{\text {position }}+\alpha_{\text {score }} \sum_{k=1}^{K} l_{k}^{\text {score }}+\sum_{k=1}^{K} l_{k}^{\text {usp }}\tag{6}它分成三个部分,并且对于所有最近邻 K 个点进行叠加。其中:
Position Loss
这一部分 loss 主要目标是确保 A 图检测的关键点位置(经过变换后)与 B 图检测的关键点位置是相同的,也就是不同视角下点的位置的稳定性:
l_{k}^{\text {position }}=d_{k}\tag{7}
Score Loss
这一部分 loss 主要目标是确保 A 图与 B 图相同点的得分具有相似性,也就是不同视角下点的置信度是一致的:
l_{k}^{\mathrm{score}}=\left(\hat{s}_{k}^{\mathrm{A}}-\hat{s}_{k}^{\mathrm{B}}\right)^{2}\tag{8}
Unsupervised Point Loss
这一部分 loss 主要目标是确保网络预测的 score (置信度)反映了关键点坐标可复现性(repeatable)的概率,例如不同视角下复现率更高的点它的 score 也更高:
l_{k}^{\text {usp }}=\hat{s}_{k}\left(d_{k}-\bar{d}\right)\tag{9}
其中 \hat{s}_{k} 表示相同点在 A 和 B 图的平均分数:
\hat{s}_{k}=\frac{\hat{s}_{k}^{\mathrm{A}}+\hat{s}_{k}^{\mathrm{B}}}{2}\tag{10}
而 \bar{d} 表示相同点在所有最近邻中的平均位置:
\bar{d}=\frac{1}{K} \sum_{k=1}^{K} d_{k}\tag{11}
3.2 Uniform point predictions \mathcal{L}^{uni\_xy}
如果只是用上面的 Loss 进行无监督训练,容易产生一些有缺陷(artifact)的关键点。例如下图:
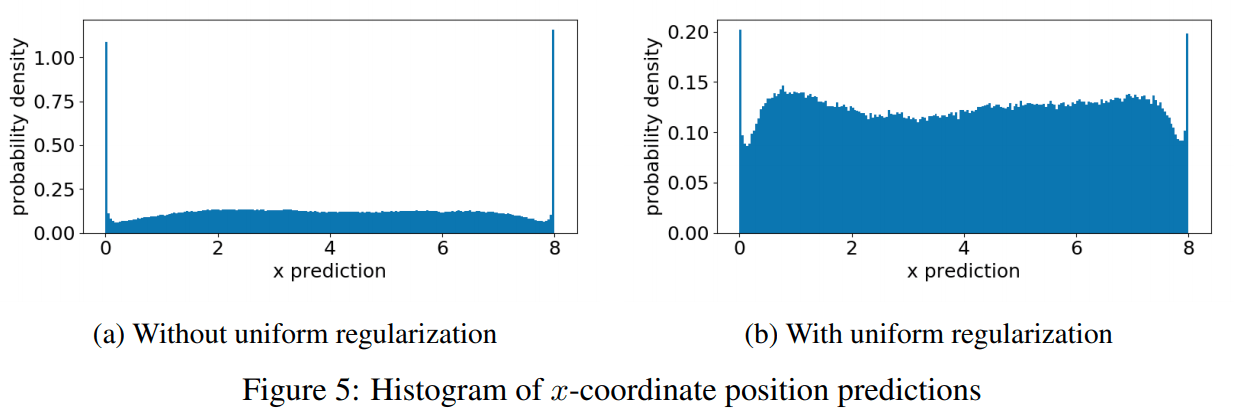
大部分预测点的 offset 坐标可能都会集中在块的边缘(0和8)如图(a)所示,如果加入均匀 loss 则会相对比较分散,如图(b)所示。显然对于一个块内的点 offset 应该是均匀分布才比较合理。
Uniform point predictions \mathcal{L}^{uni\_xy} 正是为解决这一问题而设计。它的定义如下:
\begin{aligned}\mathcal{L}^{\text {uni\_xy}} &=\alpha_{\text {uni\_xy}}\left(\mathcal{L}^{\text {uni\_x}}+\mathcal{L}^{\text {uni\_y}}\right) \\\mathcal{L}^{\text {uni\_x}} &=\sum_{i=1}^{M}\left(x_{i}^{\text {sorted }}-\frac{i-1}{M-1}\right)^{2} \\\mathcal{L}^{\text {uni\_y}} &=\sum_{i=1}^{M}\left(y_{i}^{\text {sorted }}-\frac{i-1}{M-1}\right)^{2}\tag{12}\end{aligned}3.3 Descriptor \mathcal{L}^{desc}
描述子 Loss 定义如下,就是 hinge loss:
\begin{aligned}\mathcal{L}^{\mathrm{desc}} &=\sum_{i=1}^{M^A} \sum_{j=1}^{M^B} l_{i j}^{\mathrm{desc}} \\l_{i j}^{\mathrm{desc}} &=\lambda_{d} \cdot c_{i j} \cdot \max \left(0, m_{p}-\mathbf{f}_{i}^{\mathrm{A}^{T}} \mathbf{f}_{j}^{\mathrm{B}}\right) \\&+\left(1-c_{i j}\right) \cdot \max \left(0, \mathbf{f}_{i}^{\mathrm{A}^{T}} \mathbf{f}_{j}^{\mathrm{B}}-m_{n}\right) \\\tag{13}\end{aligned}3.4 Decorrelate descriptor \mathcal{L}^{decorr}
Decorrelate(去相关) descriptor loss \mathcal{L}^{decorr} 用于对抗过拟合和提升描述子部分的紧致程度。设有一个描述子相关性矩阵 \mathbf{R}^{b}=\left[r_{i j}^{b}\right]_{F \times F},则 \mathcal{L}^{decorr} 的定义如下:
\mathcal{L}^{\mathrm{decorr}}=\sum_{i \neq j}^{F}\left(r_{i j}^{\mathrm{A}}\right)+\sum_{i \neq j}^{F}\left(r_{i j}^{\mathrm{B}}\right) \\\tag{14}其中:
r_{i j}^{b}=\frac{\left(\mathbf{v}_{j}^{b}-\bar{v}_{j}^{b}\right)^{T}\left(\mathbf{v}_{i}^{b}-\bar{v}_{i}^{b}\right)}{\sqrt{\left(\mathbf{v}_{j}^{b}-\bar{v}_{j}^{b}\right)^{T}\left(\mathbf{v}_{i}^{b}-\bar{v}_{i}^{b}\right)} \sqrt{\left(\mathbf{v}_{j}^{b}-\bar{v}_{j}^{b}\right)^{T}\left(\mathbf{v}_{i}^{b}-\bar{v}_{i}^{b}\right)}}\tag{15}上式中 \mathbf{v}_{i}^{b} 是一个 \mathbf{M}_b \times 1 维列向量,它代表了 \mathbf{F}_b 中的第 i 列。\bar{v}_{i}^{b} 代表 \mathbf{v}_{i}^{b} 的均值。
4 实验
实验结果自然是很喜人的(不喜人还发啥呢),在速度和 SuperPoint 相差无几情况下,在各种测试集上基本都超过了 SuperPoint 和其他几个网络。详细实验细节文章是比较丰富的,具体建议仔细阅读原文,这里仅摘抄几个主要结论:
4.1 参数设定
作者使用 MSCOCO 数据进行训练总计 118,287 张图片。试验中用到的参数如下:
| 参数名 | 参数值 |
| 输入 | 320x240x3 |
| normalize | -0.5再x0.225 |
| batch size | 5 |
| optimizer | Adam |
| \epsilon_{correspond} | 4 |
| m_p | 1 |
| m_n | 0.2 |
| \delta_d | 250 |
| \alpha_{usp} | 1 |
| \alpha_{position} | 1 |
| \alpha_{score} | 2 |
| \alpha_{uni\_xy} | 100 |
| \alpha_{desc} | 0.001 |
| \alpha_{decorr} | 0.03 |
4.2 对比实验
对于论文中提到的几种策略作者做了对比试验:
C1 表示在 descriptor 部分增加差值,这一操作提升了 matching score(对应 1.4);
C2 表示在 detector 部分增加 Uniform point predictions,这一操作提升了 repeatability、homography 精度并降低了 localization error(对应 3.2);
C3 表示在 descriptor 部分增加 Decorrelate,这一操作不仅提升了 repeatability ,也提升了全局性能。
C4 表示同时使用 C1 C2 C3 策略。
实验结果如下表:
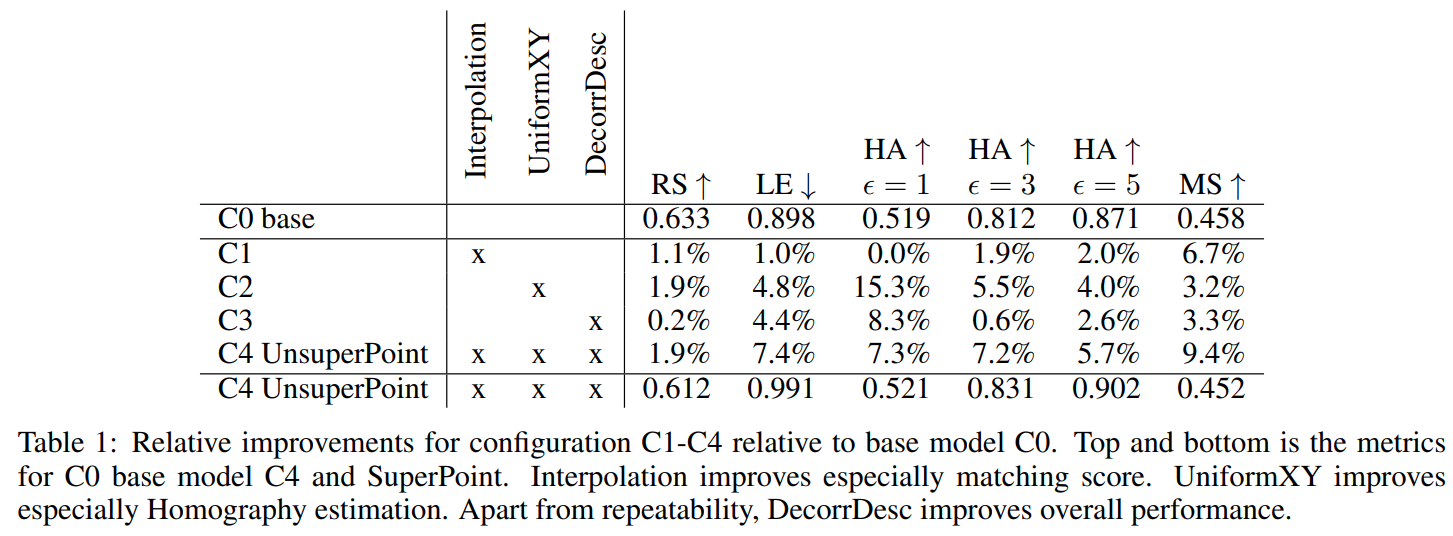
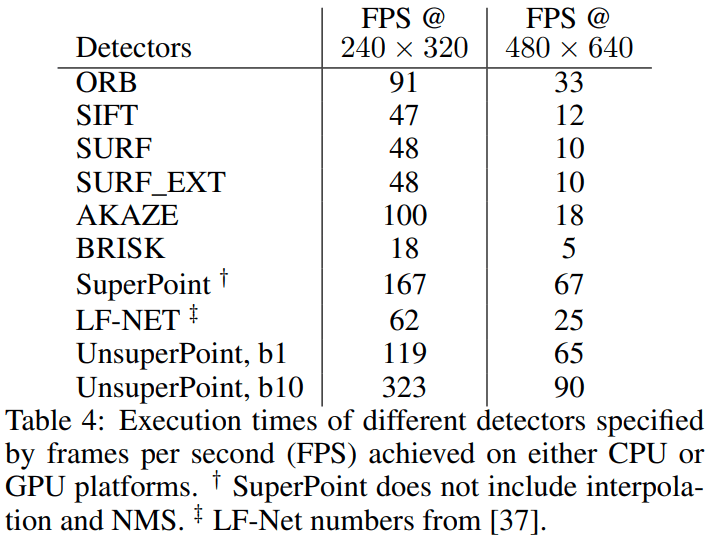
4.3 速度
SuperPoint, UnsuperPoint and LF-Net 速度测试环境为: GPU (GeForce Titan X),其他在 CPU (Intel i7-7700HQ).
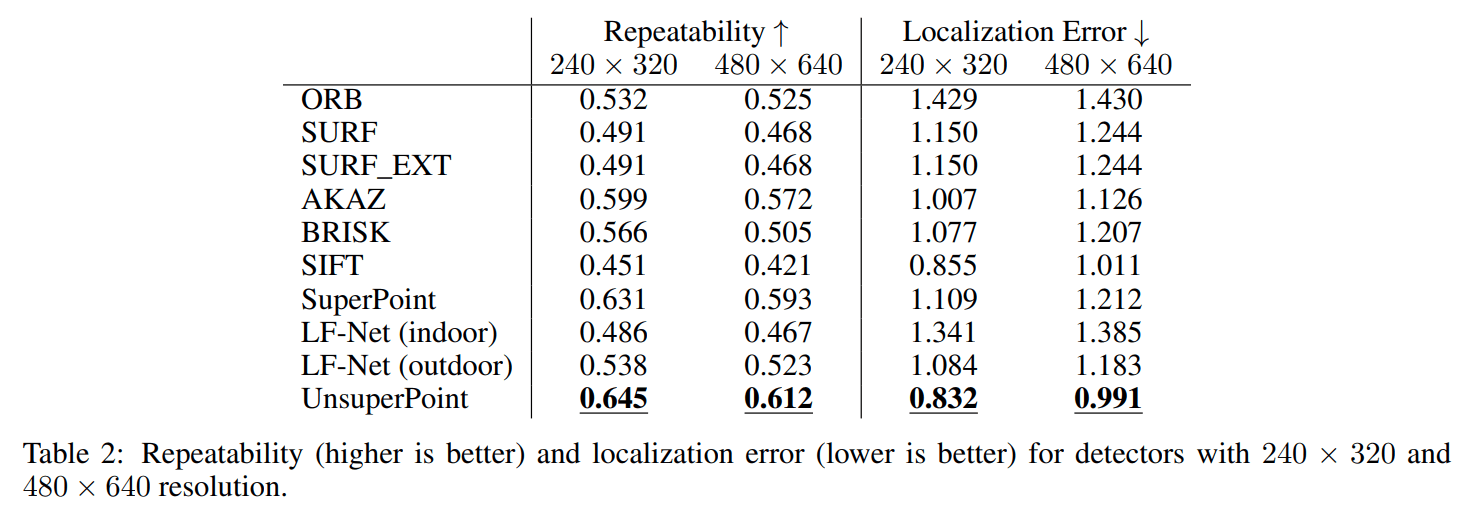
4.4 Repeatability and localization error
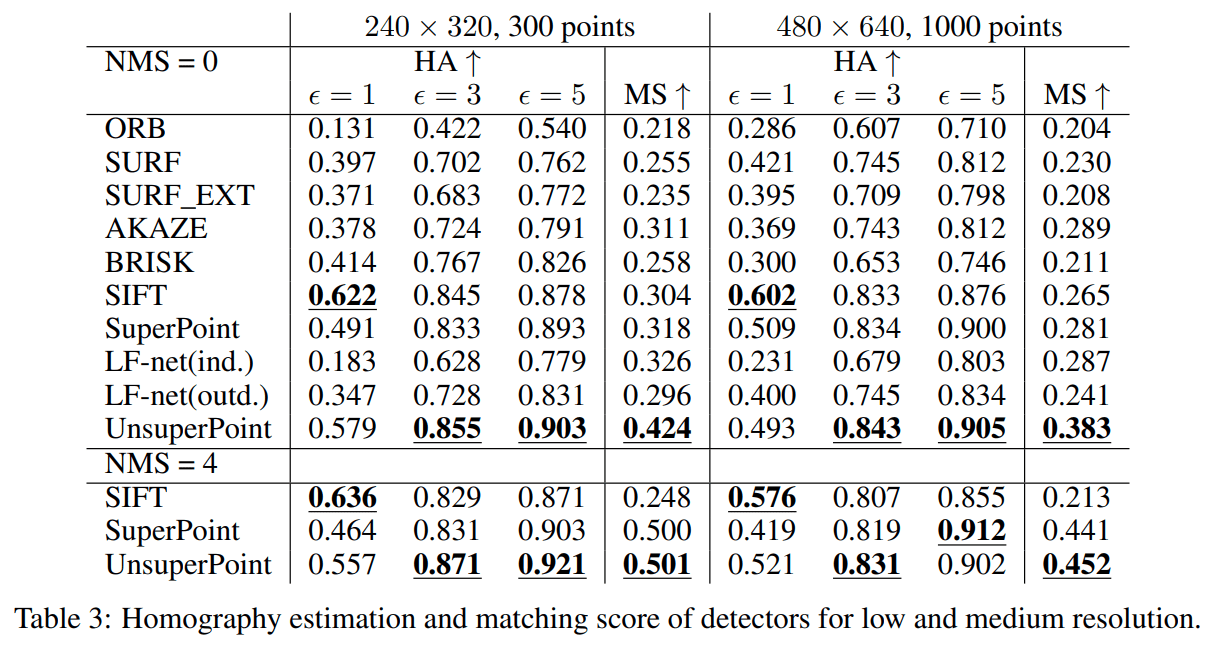
4.5 Homography estimation and matching score
个人小结
本文最主要的贡献在于无监督的方式,在实际环境中的确非常实用。但是对于怎么学习出 detector 还是比较疑惑。由于作者没有提供源码,预计复现还是比较不容易的。
相关材料
论文
源码(第三方示例)
https://github.com/791136190/UnsuperPoint_PyTorch
https://github.com/RPFey/UnsuperPoint
作者给的参数有问题。。感觉无法复现
github链接失效了,博主能提供新地址吗,非常感谢
博主您好,github链接失效了,能再提供一下链接吗,非常感谢。2249558536@qq.com
看到两个其他人的复现,更新了下,看看有没有用