DTAM 中的 Cost Volume 笔记
DTAM 是比较经典的基于 RGBD 的 SLAM 算法,其中的 Cost Volume 部分也是后续比较常见的模块,这里进行一下记录。
1 定义说明
定义 \mathrm{T}_{w c} \in \mathbb{S E}(3) 表示从相机坐标系 c 到世界坐标系 w 的变换矩阵:
\begin{equation}\mathrm{T}_{w c}=\left(\begin{array}{cc}\mathrm{R}_{w c} & \mathbf{t}_w \\\mathbf{0}^T & 1\end{array}\right)\end{equation}
其中 \mathrm{R}_{w c} \in \mathbb{SO}(3) 表示旋转矩阵, \mathbf{t}_w 表示平移向量。
则对于空间中一个点具有如下变换关系:
\begin{equation}\mathbf{x}_w=\mathrm{T}_{w c} \mathbf{x}_c\end{equation}
以及投影操作:
\begin{equation}\mathbf{u} = \pi\left(\mathbf{x}_c\right)=(x / z, y / z)^{\top}\end{equation}
反投影操作:
\begin{equation}\mathbf{x}=\pi^{-1}(\mathbf{u}, d)\end{equation}
其中 d=\boldsymbol{\xi}(\mathbf{u}) 表示像素 \mathbf{u} 对应的逆深度。
则 2D 和 3D 映射关系为:
\begin{equation}\begin{gathered}\mathbf{x}=\pi^{-1}(\mathbf{u}, d) \\\pi^{-1}(\mathbf{u}, d)=\frac{1}{d} \mathrm{K}^{-1} \dot{\mathbf{u}} \\\dot{\mathbf{u}}=(u, v, 1)^T\end{gathered}\end{equation}
2 Cost Volume
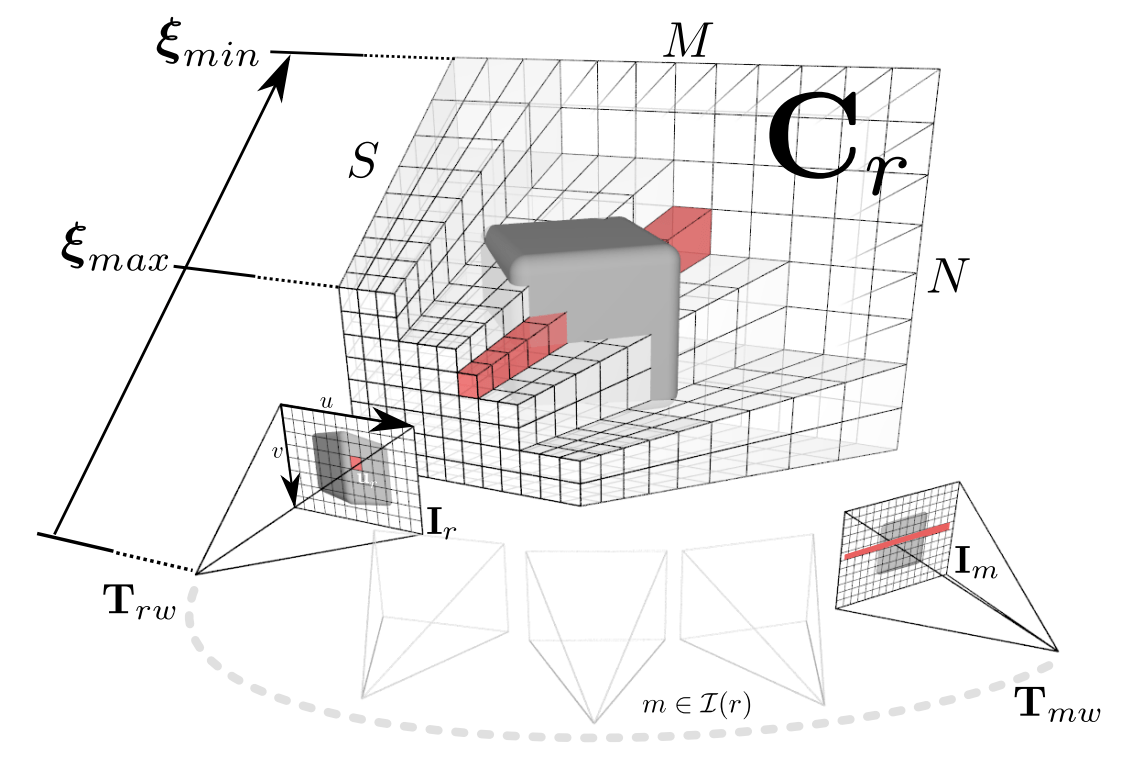
DTAM 中计算 Cost Volume 的方式如上图所示。
对一个关键帧序号 r ,其对应世界到相机坐标系变换记为 \mathrm{T}_{r w};逆深度图记为 \boldsymbol{\xi}_r: \Omega \rightarrow \mathbb{R};RGB 图像记为 \mathbf{I}_r: \Omega \rightarrow \mathbb{R}^3,\Omega \subset \mathbb{R}^2 为像素坐标集合。
对关键帧 \mathbf{I}_r,其取较短基线(共视区域差异不要太大)的关键帧集合 m \in \mathcal{I}(r),则我们记它的 Cost Volume 为:
\begin{equation}\mathbf{C}_r(\mathbf{u}, d)=\frac{1}{|\mathcal{I}(r)|} \sum_{m \in \mathcal{I}(r)}\left\|\rho_r\left(\mathbf{I}_m, \mathbf{u}, d\right)\right\|_1\end{equation}
其中:
\begin{equation}\rho_r\left(\mathbf{I}_m, \mathbf{u}, d\right)=\mathbf{I}_r(\mathbf{u})-\mathbf{I}_m\left(\pi\left(\mathrm{KT}_{m r} \pi^{-1}(\mathbf{u}, d)\right)\right)\end{equation}
根据亮度一致假设,我们优化目标为使得光度误差 \rho 最小的表面逆深度 d,认为该逆深度对应的表面就是对应的真实物体表面。
参考文献
[1] https://www.semanticscholar.org/paper/DTAM%3A-Dense-tracking-and-mapping-in-real-time-Newcombe-Lovegrove/7633c7470819061477433fdae15c64c8b49a758b