论文笔记:Online Invariance Selection for Local Feature Descriptors
本篇文章是 ECCV 2020 Oral ,来自 ETH 的最新大作。本文主要侧重点在于通过神经网络的方式在线选择不变性的局部特征。通过很少的计算量增加,该方法可以比较通用地扩展到各种检测和描述子中,极大地提升实际场景的匹配效果。
主要创新点如下:
-
使用一个网络通过多任务学习的方式学习出适应多种变化组合的描述子
-
提出了一种基于 meta descriptor 的轻量级在线选择不变性描述子的方式
-
本文提出的多任务学习变化描述子以及在线选择不变性描述子的方式,可以拓展到任何传统或者基于 learning 的描述子上,具有很强的通用性。
1 Learning the best invariance for local descriptors
为了说明选择最佳不变性描述子的意义,作者举了个例子:

如上图所示,在纯旋转情况下 SIFT 可以有很好的表现,但是在没有旋转时, Upright SIFT (主方向固定为 (0, 1)) 又比 SIFT 表现好。这样我们显然地希望有一个自动的机制能够选择用哪一种描述子匹配。右侧就是本算法自动选择的结果,可以看出在两种不同情况下,都取得了很好的匹配效果。文中最后也给了 HPatches 数据集的评测结果:

1.1 Disentangling invariance for local descriptors
有非常多的因素会影响到一个 descriptor 匹配的效果,本文中选择了影响最大的两个:rotation(旋转)和 illumination (光照)。相比之前的描述子希望通过一个 descriptor 同时适应所有情况不同,本文生成了四种组合的描述子按照这两种影响因素的排列组合分别对应如下四种变化:
| No. | rotation | illumination |
|---|---|---|
| 1 | variance | variance |
| 2 | invariance | variance |
| 3 | variance | invariance |
| 4 | invariance | invariance |
Network architecture
网络设计参考了 SuperPoint 做了很多改进,整体结构图如下:

从共享的 CNN backbone 生成 Semi dense features 后,划分成 4 个 heads 分别对应上面所提到的4种不同的变化组合。
Dataset preparation
需要准备如下数据:
I^A:anchor image,从数据库中选择的原图
I^V:variant image,包含无旋转的 Homography,亮度变化与原图相同
I^I:invariant image,包含与原图不同的旋转和亮度变化
Training losses
本文使用 SIFT 作为特征点(任意特征点均可),通过如下方式定义 Loss:
图像对 I^a 和 I^b ,二者间的 Homography 矩阵为 \mathcal{H},对应点具有如下关系 \mathbf{x}_{1 . . n}^{b}=\mathcal{H}\left(\mathbf{x}_{1 . . n}^{a}\right)。我们将通过下面的描述定义一种通用的 triplet loss 表达方式。
二者提取的 descriptors 分别为 \mathbf{d}_{1 . . n}^{a} 和 \mathbf{d}_{1 . . n}^{b} (L2 normalized)。二者距离定义为:
p_{i}=\operatorname{dist}\left(\mathbf{x}_{i}^{a}, \mathbf{x}_{i}^{b}\right)\tag{1}
进一步地,triplet loss 会增加对应点对 \mathbf{x}_i^a 以及其在 I^b 中最近的负样本 \mathbf{x}_{n_b(i)}^b 之间的距离,当然对于 \mathbf{x}_i^b 同理。因此这一部分定义为:
n_{i}=\min \left(\operatorname{dist}\left(\mathbf{x}_{i}^{a}, \mathbf{x}_{n_{b}(i)}^{b}\right), \operatorname{dist}\left(\mathbf{x}_{i}^{b}, \mathbf{x}_{n_{a}(i)}^{a}\right)\right)\tag{2}
其中 详细定义为:
n_{b}(i)=\arg \min _{j \in[1, n]}\left(\operatorname{dist}\left(\mathbf{x}_{i}^{a}, \mathbf{x}_{j}^{b}\right)\right) \text { s.t. }\left\|\mathbf{x}_{i}^{a}-\mathbf{x}_{j}^{b}\right\|_{2}>T\tag{3}
给定 margin M 则典型的 triplet margin loss 定义为:
L_{T}\left(I^{a}, I^{b}, \operatorname{dist}\right)=\frac{1}{n} \sum_{i=1}^{n} \max \left(M+\left(p_{i}\right)^{2}-\left(n_{i}\right)^{2}, 0\right)\tag{4}
在本文中对于 invariant decscriptor 的 loss L_{I} 是上述 L_{T} 一个特例。分别对应 I^A 和 I^I:
L_{I}=L_{T}\left(I^{A}, I^{I},\left\|\mathbf{d}^{A}-\mathbf{d}^{I}\right\|_{2}\right)\tag{5}
对于 variant descriptor 的 loss L_{V} 是一个包含 I^A、I^V 和 I^I 三幅图提取信息的整体 triplet loss,它的定义如下:
L_{V}=\frac{1}{n} \sum_{i=1}^{n} \max \left(f M+\left\|\mathbf{d}_{i}^{A}-\mathbf{d}_{i}^{V}\right\|_{2}^{2}-\left\|\mathbf{d}_{i}^{A}-\mathbf{d}_{i}^{I}\right\|_{2}^{2}, 0\right)\tag{6}
其中 f 是控制表示 I^A 和 I^I 之间差异的因子,对于旋转差异而言 f=\min \left(1, \frac{\theta_{I}}{\theta_{\max }}\right),\theta_{I } 表示 I^A 和 I^I 之间的绝对旋转角度;\theta_{\max } 是一个超参数表示多大的旋转才被认为是负样本。这一参数控制使得只有发生较大旋转时才会对 loss 进行惩罚(也就是较大旋转时 loss 的 margin 变大);由于在实际图像中我们无法定义亮度变化的差异,因此对于只有亮度变化时我们设 f=1。
最终的 loss 就是 4 种不同组合 loss 相加,对于变化和不变的 descriptor 分别使用 L_{V} 或者 L_{I}:
L_{l}=\frac{1}{|\mathcal{D}|} \sum_{d \in \mathcal{D}} L_{I / V}(d)\tag{7}1.2 Online selection of the best invariance
有了上面的方法训练4种不同的 descriptor 后,我们如何在实际场景的匹配中选择使用呢?一个最简单的方式就是挨个匹配一遍,然后选择距离最近的那个匹配。但是这种方式并没有更好地利用上下文信息和4个 descriptors,未必是最好的方法。本文旨在提出一种更好的在线选择机制使得获得更好的匹配。
Meta descriptors
首先我们将图像划分成 c \times c 的网格(本文中使用的是 3 \times 3),每个网格中的 descriptors 通过 NetVLAD 获得一个聚类中心作为 meta descriptors。这样对于每个划分的网格,最终获得4个 meta descriptors,这些 meta descriptors 同样也经过了 L2 normalized。
其次用软决策代替了硬决策,权重由 meta descriptors 进行计算得到,也就是相当于用 meta descriptors 作为所有 descriptors 的代表。通过 softmax 分别给每个 descriptor 设置了权重,最终的距离由4个加权和得到。
\operatorname{dist}\left(\mathbf{x}^{a}, \mathbf{x}^{b}\right)=\sum_{i=1}^{4} \frac{\exp \left(\left(\mathbf{m}_{i}^{a}\right)^{\top} \cdot \mathbf{m}_{i}^{b}\right)}{\sum_{j=1}^{4} \exp \left(\left(\mathbf{m}_{j}^{a}\right)^{\top} \cdot \mathbf{m}_{j}^{b}\right)}\left\|\mathbf{d}_{i}^{a}-\mathbf{d}_{i}^{b}\right\|_{2}\tag{8}
其中 m 在最开始聚类时已经算好,根据当前 grid 对应的位置即可找到。
Training Loss
对于 4 个 NetVLAD 层的训练只需使用 weakly supervised 方法即可,不需要监督。同样使用上面提到的 triplet loss,只不过这里的 descriptor 换成了 meta descriptors。
L_m = L_T(I^A,I^I,\operatorname{dist})\tag{9}
最终两部分总的 Loss 为加权和:
1.3 Training details
这部分主要是网络结构和Loss参数细节,略过,看论文即可。
2 Experiments
本文实验做得相当全面,通过 Homography estimation 、Precision 和 Recall 三个指标进行了多组实验。
Ablation study
这部分作者做了下面一些对比说明 Online Selection 的有效性:

其中:
-
Best of the 4 是对 4 种 descriptors 都进行匹配,然后就选距离最小的一类;
-
Greedy 是每个 keypoint 都分别对 4 种 descriptor 进行匹配然后每个都找距离最近的;
-
Hard assignment 是不使用权重,直接通过 meta descriptor 选择固定的一类。
-
No tiling 和 5x5 是表示划分网格的多少。
-
Single desc 表示仍然采用这个网络进行训练得到 4个 descriptor 但将4个 concat 成1个并对所有光照和旋转进行训练。
最终可以看出本文中提出的策略的有效性,每个步骤都起了一定的涨点作用。
Descriptor evaluation on HPatches
在 HPatches 数据集中的实验如下:

Evaluation in challenging and cross-modal situations
为了包含更大的光照、视角变化,作者基于 day-night image matching dataset 进行了增强得到了一个更加困难的数据集(Rotated Day-Night Image Matching (RDNIM)),下载地址如下:
Polybox:
https://www.polybox.ethz.ch/index.php/s/P89YkZyOfdhmdPN
百度网盘:
链接: https://pan.baidu.com/s/1TFWWpUqGjC3u_0mms9Lunw 提取码: jjnf
在这个更加困难的数据集中得到了如下结果(下面最新的结果来自 github):
Comparison to the state of the art on the RDNIM dataset, using SuperPoint keypoints for all methods:
| Day reference | Night reference | |||||
|---|---|---|---|---|---|---|
| Homography estimation | Precision | Recall | Homography estimation | Precision | Recall | |
| Root SIFT | 0.121 | 0.188 | 0.112 | 0.141 | 0.238 | 0.164 |
| HardNet | 0.199 | 0.232 | 0.194 | 0.262 | 0.366 | 0.323 |
| SOSNet | 0.178 | 0.228 | 0.203 | 0.211 | 0.297 | 0.269 |
| SuperPoint | 0.146 | 0.195 | 0.178 | 0.182 | 0.264 | 0.255 |
| D2-Net | 0.094 | 0.195 | 0.117 | 0.145 | 0.259 | 0.182 |
| R2D2 | 0.170 | 0.175 | 0.162 | 0.196 | 0.237 | 0.216 |
| GIFT | 0.187 | 0.152 | 0.133 | 0.241 | 0.236 | 0.209 |
| LISRD (ours) | 0.253 | 0.402 | 0.440 | 0.297 | 0.484 | 0.519 |
论文中的结果稍有不同:

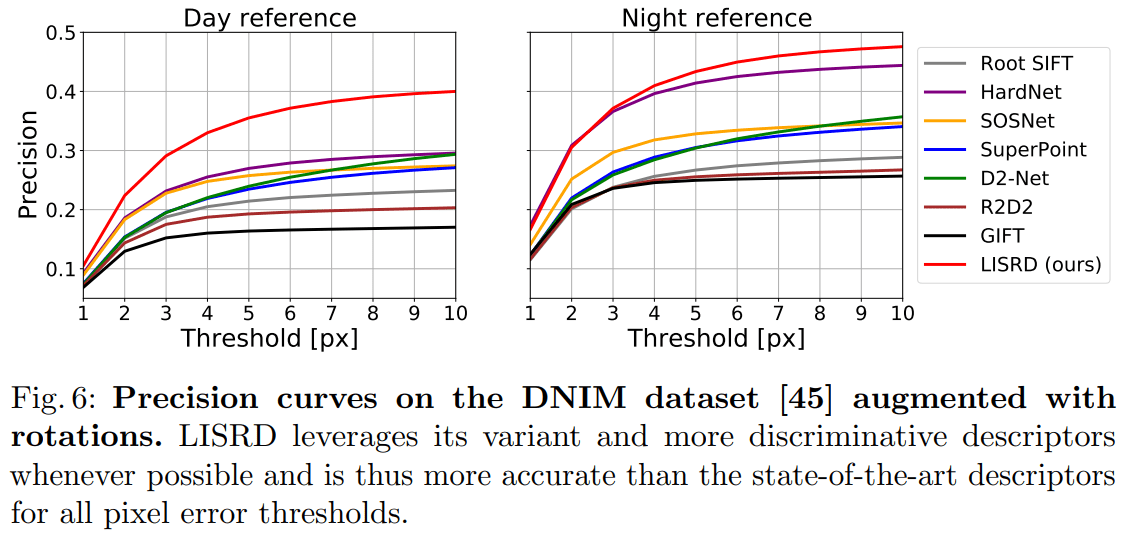
Application to localization in challenging conditions
在 Aachen Day-Night dataset 数据集上的结果:

个人小结
非常好想法,把训练一个万能的 descriptor (想想也不可能同时具备区分度和鲁棒性),改成训练几种主要的集合,然后对于实际场景进行了在线的适配。这个在线适配的过程起到了决定性的作用。
这也启发了我们也许收集所有样本然后训练出一个万能的网络不如设计生成几个针对不同场景的结果,然后在线获得它的选择性匹配。
参考材料
论文
源码
https://github.com/rpautrat/LISRD
关于原文1.2节,中间 Training loss,原文公式8,您文中公式9中 dist的计算,似乎原文表述中没有提到是把原来的local descriptors换成了meta descriptors?
原文:
> The 4 NetVLAD layers are trained with a weak supervisionbased on another instance of the triplet loss $L_T$ between $I^A$ and $I^I$ with the distance defined above:
> Thanks to this weak supervision, there is no need to explicitly supervise the meta descriptors, which would require knowing the amount of rotation and illuminationfor every tile in the image. The total loss of the network is finally a combinationof the local and meta descriptors, weighted by a factor λ:
我是【计算机视觉SLAM】的公众号的博主,很早就关注了博主,您写的文章质量很高,申请能够转载您的文章,谢谢~
没问题,请注明作者和本站链接,同时不要用于商业用途。