論文メモ：NeRF: 視点合成のためのニューラル放射場としてシーンを表現

2021年11月1日

Table of Contents

NeRF は ECCV 2020 の Oral であり、非常に大きな影響を与え、神経ネットワークに基づく暗黙的な表現を用いてシーンを再構築する新しいアプローチを基礎から生み出したと言えます。そのシンプルなアイデアと完璧な効果により、現在でも多くの 3D 関連の研究がこれを基盤としています。
NeRF が行うタスクは Novel View Synthesis（新しい視点の合成）であり、いくつかの既知の視点からシーンを観測（カメラの内外パラメータ、画像、ポーズなど）し、任意の新しい視点で画像を合成します。従来の方法では、このタスクは通常、3D 再構築を行ってからレンダリングする方法で実現されていましたが、NeRF は明示的な 3D 再構築プロセスを行わず、内外パラメータに基づいて直接新しい視点のレンダリング画像を得ることを目指しています。この目的を達成するために、NeRF は神経ネットワークを 3D シーンの暗黙的な表現として使用し、従来の点群、メッシュ、ボクセル、TSDF などの方法に代わり、このようなネットワークを通じて任意の角度や位置からの投影画像を直接レンダリングすることができます。

NeRF のアイデアは比較的シンプルで、入力視点の画像の各ピクセルの光線に対して密度（不透明度）の積分を行い、ボクセルレンダリングを行います。その後、そのピクセルのレンダリングされた RGB 値と真値を比較して Loss とします。論文で設計されたボクセルレンダリングは完全に微分可能であるため、このネットワークは学習可能です。

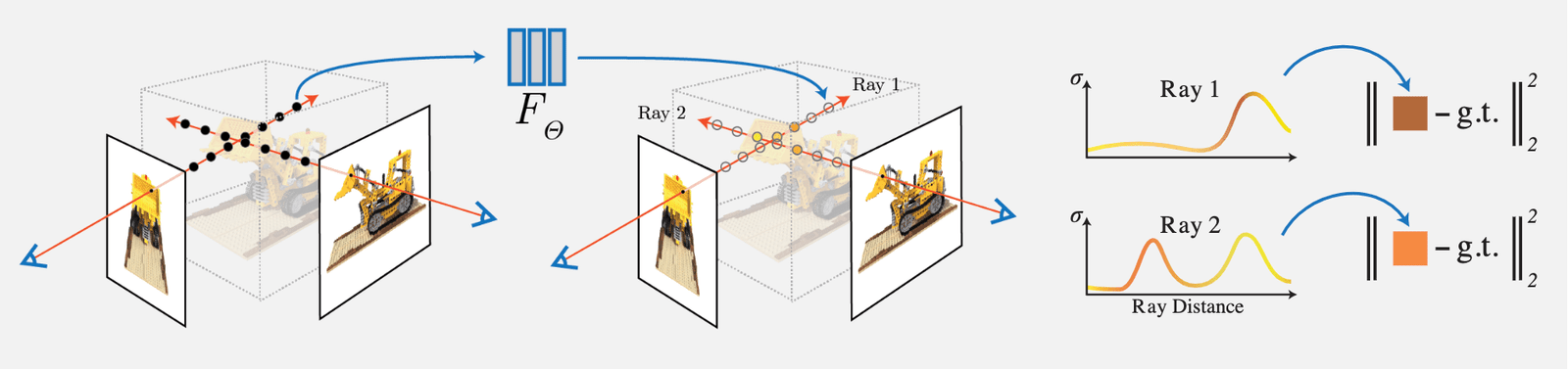
主な作業と革新点は以下の通りです：
1）複雑なジオメトリとマテリアルの連続シーンを表現するために、5D 神経放射場 (Neural Radiance Field) を使用する方法を提案しました。この放射場は MLP ネットワークを使用してパラメータ化されています。
2）古典的なボクセルレンダリング (Volume Rendering) に基づく改良された微分可能なレンダリング方法を提案し、微分可能なレンダリングを通じて RGB 画像を取得し、これを最適化の目標とします。この部分には、分層サンプリングを使用した高速化戦略が含まれており、MLP の容量を可視コンテンツ領域に割り当てます。
3）各 5D 座標をより高次元の空間にマッピングする位置エンコーディング (Position Encoding) 方法を提案し、これにより神経放射場が高周波の詳細をよりよく表現できるようになります。

1 Neural Radiance Field Scene Representation (神経放射場に基づくシーン表現)

NeRF は連続的なシーンを 5D ベクトル値関数（vector-valued function）として表現します。具体的には：

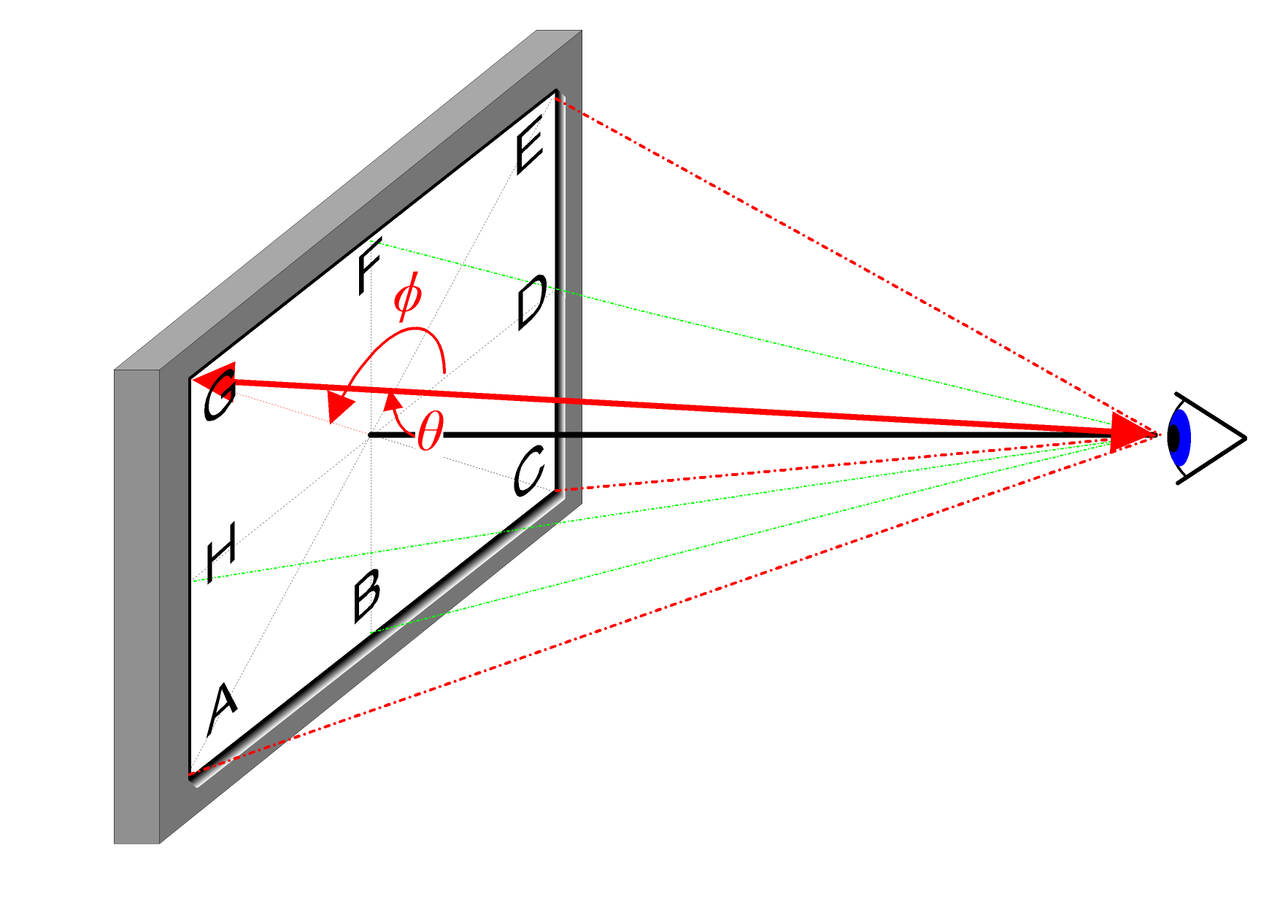
入力は：3D 位置 $\mathbf{x}=(x, y, z)$ と 2D 視点方向 $(\theta, \phi)$
出力は：放射色 $\mathbf{c}=(r, g, b)$ と体積密度（不透明度） $\sigma$ 。

2D 視点方向については、以下の図で直感的に説明できます：

実際の実装では、視点方向は 3D デカルト座標系の単位ベクトル $\mathbf{d}$ で表されます。つまり、画像内の任意の位置とカメラの光心を結ぶ線です。このマッピングを MLP 全結合ネットワークで表現します：
$\begin{equation}F_{\Theta}:(\mathbf{x}, \mathbf{d}) \rightarrow(\mathbf{c}, \sigma)\end{equation}$

このようなネットワークのパラメータ $\Theta$ を最適化することで、5D 座標を入力として対応する色と密度を出力するマッピングを学習します。

多視点の表現をネットワークに学習させるために、以下の 2 つの合理的な仮定を行います：

体積密度（不透明度） $\sigma$ は 3D 位置 $\mathbf{x}$ のみに依存し、視点方向 $\mathbf{d}$ には依存しません。物体の異なる位置の密度は観察角度に依存しないべきであり、これは明らかです。
色 $\mathbf{c}$ は 3D 位置 $\mathbf{x}$ と視点方向 $\mathbf{d}$ の両方に依存します。

体積密度 $\sigma$ を予測するネットワーク部分の入力は位置 $\mathbf{x}$ のみであり、色 $\mathbf{c}$ を予測するネットワークの入力は視点と方向 $\mathbf{d}$ です。具体的な実装では：

MLP ネットワーク $F_{\Theta}$ は、まず 8 層の全結合層（ReLU 活性化関数を使用し、各層に 256 チャンネル）を使用して 3D 座標 $\mathbf{x}$ を処理し、 $\sigma$ と 256 次元の特徴ベクトルを取得します。
この 256 次元の特徴ベクトルを視点方向 $\mathbf{d}$ と結合し、別の全結合層（ReLU 活性化関数を使用し、各層に 128 チャンネル）に入力し、方向に依存する RGB 色を出力します。

以下は、論文中で示されたネットワーク構造の例です：

図 3 は、ネットワークが非ランバート体効果（non-Lambertian effects）を表現できることを示しています。図 4 は、トレーニング時に視点（View Dependence）の入力がない場合（ $\mathbf{x}$ のみの場合）、ネットワークがハイライト効果を表現できないことを示しています。

2 Volume Rendering with Radiance Fields (放射場を用いたボクセルレンダリング)

2.1 古典的なレンダリング方程式

本文中の Volume Rendering と Radiance Field の概念を理解するために、まずグラフィックスの基本的なレンダリング方程式を振り返ります：
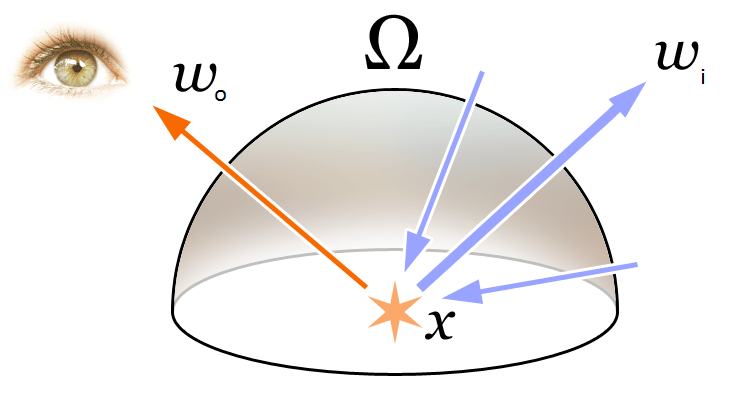
$\begin{equation}\begin{array}{l}L_{o}(\boldsymbol{x}, \boldsymbol{d}) &=L_{e}(\boldsymbol{x}, \boldsymbol{d})+\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \left(\boldsymbol{\omega}_{i}, \boldsymbol{n}\right) d \boldsymbol{\omega}_{i}\\&=L_{e}(\boldsymbol{x}, \boldsymbol{d})+\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \cos \theta d \boldsymbol{\omega}_{i}\end{array}\end{equation}$

上記の図のように、レンダリング方程式は 3D 空間位置 $\mathbf{x}$ の方向 $\mathbf{d}$ における放射（出射光） $L_{o}(\boldsymbol{x}, \boldsymbol{d})$ を表現しています。この放射は、その点からの放射（発射光） $L_{e}(\boldsymbol{x}, \boldsymbol{d})$ と、その点で外部から反射された放射（反射光）の和として表されます。具体的には：

$L_{e}(\boldsymbol{x}, \boldsymbol{d})$ は、 $\mathbf{x}$ が光源点として方向 $\mathbf{d}$ に放射する放射（発射光）を表します。
$\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \cos \theta d \boldsymbol{\omega}_{i}$ は、入射方向半球の積分を表します。
$f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right)$ は散乱関数で、入射方向から出射方向への放射の反射率を表します。
$L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right)$ は、 $\boldsymbol{\omega}_{i}$ 方向から受け取る放射を表します。
$\boldsymbol{n}$ は 3D 空間位置 $\mathbf{x}$ の法線であり、 $\theta$ は $\boldsymbol{\omega}_{i}$ と $\boldsymbol{n}$ の間の角度です。明らかに、 $\left(\boldsymbol{\omega}_{i}, \boldsymbol{n}\right)=\cos \theta$ です。

放射の概念を簡単に理解すると、物理学では光は電磁放射であり、電磁波の波長 $\lambda$ と周波数 $\nu$ の関係式は次の通りです：
$\begin{equation}c=\lambda \nu\end{equation}$

つまり、両者の積は光速 $c$ です。また、可視光の色 RGB は異なる周波数の光放射がカメラに作用した結果であることがわかっています。したがって、NeRF では放射場は色の近似モデリングと見なされています。

2.2 古典的なボクセルレンダリング方法

私たちが通常接するレンダリングには、メッシュレンダリングやボクセルレンダリングなどがあります。雲や煙などのエフェクトには、ボクセルレンダリングがよく使用されます：

私たちの 5D 神経放射場は、シーンをその空間内の任意の点におけるボクセル密度と方向性のある放射輝度として表現します。ボクセル密度 $\sigma(\mathbf{x})$ は、光線が位置 $\mathbf{x}$ に留まる無限小粒子の確率（または、光線がこの点を通過した後に停止する確率）として定義されます。古典的な立体レンダリングの原理を使用して、シーンを通過する任意の光線の色をレンダリングできます。

したがって、ある視点 $\mathbf{o}$ から発せられる方向 $\mathbf{d}$ の光線が $t$ 時点で到達する点は次の通りです：
$\begin{equation}\mathbf{r}(t)=\mathbf{o}+t \mathbf{d}\end{equation}$
この方向に沿って $(t_n, t_f)$ の範囲で色を積分し、最終的な色値 $C(\mathbf{r})$ を得ます：

\begin{equation}C(\mathbf{r})=\int_{t_{n}}^{t_{f}} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_{n}}^{t} \sigma(\mathbf{r}(s)) d s\right)\end{equation}

関数 $T(t)$ は、光線が $t_n$ から $t$ までの間に累積した透明度（Accumulated Transmittance）を表します。言い換えれば、光線が $t_n$ から $t$ までの間に粒子に当たらずに通過する確率です。この定義に基づいて、ビューのレンダリングは $C(\mathbf{r})$ の積分として表現されます。これは、仮想カメラが各ピクセルを通過するカメラ光線によって得られる色です。

関数 $\sigma(\mathbf{x})$ （ボリューム密度 $\sigma(\mathbf{x})$ は、光線が位置 $\mathbf{x}$ にある無限小粒子で終了する微分確率として解釈できます。）

ボリュームレンダリングのためのレイキャスティング (© Zhanping Liu)。

2.3 分段サンプリング近似に基づくボクセルレンダリング方法

ただし、実際のレンダリングでは、連続的な積分を行うことはできません。積分の数値解法として求積法（quadrature）を使用します。分層サンプリング（stratified sampling）を採用して $\left[t_{n}, t_{f}\right]$ を均等に分割し、各区間で均等にサンプリングします。分割方法は次の通りです：
$\begin{equation}t_{i} \sim \mathcal{U}\left[t_{n}+\frac{i-1}{N}\left(t_{f}-t_{n}\right), t_{n}+\frac{i}{N}\left(t_{f}-t_{n}\right)\right]\end{equation}$

サンプリングされたサンプルに対して、離散的な積分方法を使用します：
$\begin{equation}\hat{C}(\mathbf{r})=\sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}, \text { where } T_{i}=\exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right)\end{equation}$
ここで、 $\delta_{i}=t_{i+1}-t_{i}$ は隣接するサンプル間の距離です。

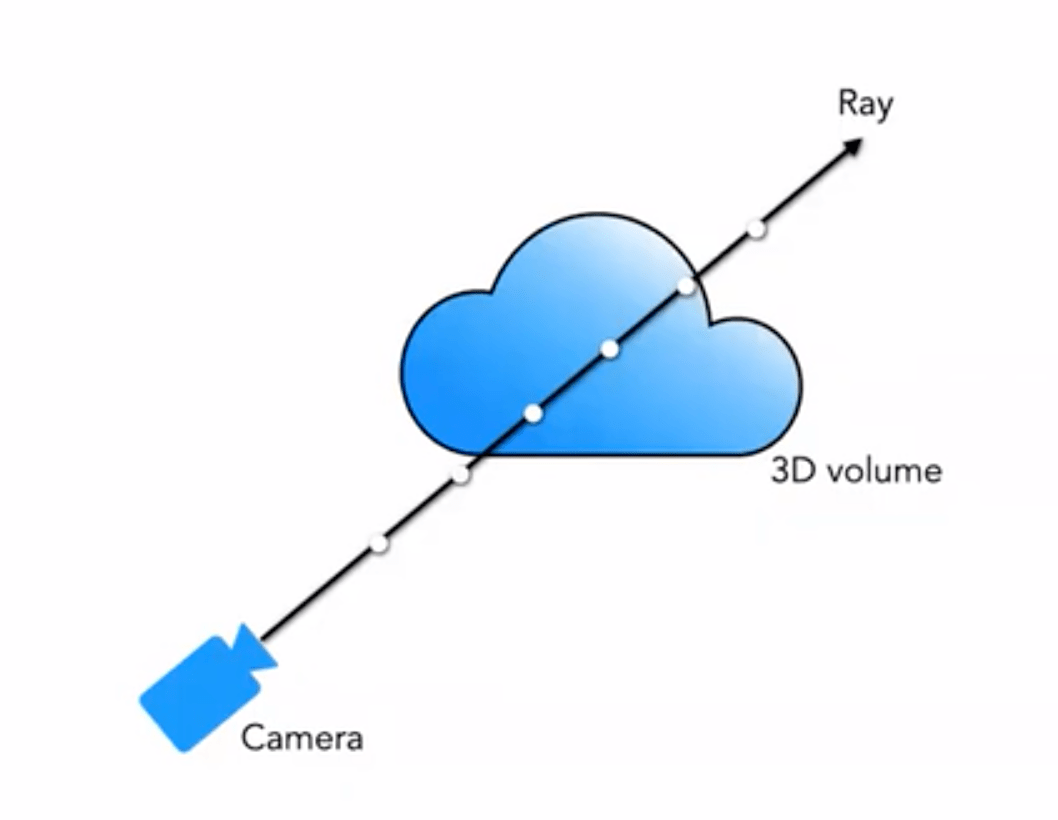
以下の図は、ボクセルレンダリングのプロセスを非常にわかりやすく示しています：

3 Optimizing a Neural Radiance Field (神経放射場の最適化)

上記の方法が NeRF の基本的な内容ですが、この方法で得られる結果は最適な効果には達しません。例えば、細部が十分に精細でない、トレーニング速度が遅いなどの問題があります。再構築の精度と速度をさらに向上させるために、以下の 2 つの戦略を導入しました：

Positional Encoding（位置エンコーディング）：この戦略により、MLP が高周波情報をよりよく表現できるようになり、豊富なディテールが得られます。
Hierarchical Sampling Procedure（金字塔サンプリング手法）：この戦略により、トレーニングプロセスで高周波情報をより効率的にサンプリングできます。

3.1 Positional Encoding（位置エンコーディング）

神経ネットワークは理論的には任意の関数に近似できるものの、実験により、MLP のみで構成された $F_{\Theta}$ では、入力 $(x, y, z, \theta, \phi)$ を完全に表現できないことがわかりました。これは Rahaman らの研究（《On the spectral bias of neural networks. In: ICML (2018) 》）が示した結論と一致しており、神経ネットワークは低周波の関数を学習する傾向があることを示しています。また、彼らの研究は、入力を高周波関数で高次元空間にマッピングすることで、データ内の高周波情報をよりよくフィットできることも示しています。

これらの発見を神経ネットワークのシーン表現タスクに応用し、 $F_{\Theta}$ を 2 つの関数の組み合わせに変更しました： $F_{\Theta}=F_{\Theta}^{\prime} \circ \gamma$ 。この方法により、ディテール表現の性能が大幅に向上します。具体的には：

$\gamma$ は $\mathbb{R}$ からより高次元の $\mathbb{R}^{2 L}$ へのエンコード関数 を表します。
$F_{\Theta}^{\prime}$ は通常の MLP ネットワークです。

本文で使用されているエンコード関数は以下の通りです：

\begin{equation}\gamma(p)=\left(\sin \left(2^{0} \pi p\right), \cos \left(2^{0} \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)\end{equation}

この関数 $\gamma(\cdot)$ は、三次元位置座標 $\mathbf{x}$ （ $[-1, 1]$ に正規化）および三次元視点方向のデカルト座標 $\mathbf{d}$ に適用されます。本論文では、 $\gamma(\mathbf{x})$ に対して $L=10$ を設定し、 $\gamma(\mathbf{d})$ に対して $L=4$ を設定します。

したがって、三次元位置座標のエンコード長は： $3 \times 2 \times 10 = 60$ であり、三次元視点方向のエンコードは $3 \times 2 \times 4 = 24$ で、ネットワーク構造図上の入力次元と対応しています。

同様に、Transformer にも類似の位置エンコード操作がありますが、本論文でのものとは根本的に異なります。Transformer では位置エンコードは入力のシーケンス情報を表すために使用されますが、ここでは入力を高次元にマッピングし、ネットワークが高周波情報をよりよく学習できるようにするために使用されます。

3.2 Hierarchical Sampling Procedure (階層的サンプリング手法)

階層的サンプリング手法は、古典的なレンダリングアルゴリズムの高速化作業から来ています。前述のボリュームレンダリング (Volume Rendering) 手法では、光線上の点をどのようにサンプリングするかが最終的な効率に影響を与えます。サンプリング点が多すぎると計算効率が低くなり、少なすぎると適切に近似できません。そこで、色の寄与が大きい点の近くで密にサンプリングし、寄与が小さい点の近くで疎にサンプリングするという自然な考え方が生まれました。この考えに基づいて、NeRF は粗から細への階層的サンプリング手法（Coarse to Fine）を提案しました。

Coarse 部分：まず粗いネットワークに対して、 $N_c$ 個の疎な点（c は Coarse を表す）をサンプリングし、式 (3) を新しい形式に修正します（重みを追加）：
$\begin{equation}\hat{C}_{c}(\mathbf{r})=\sum_{i=1}^{N_{c}} w_{i} c_{i}, \quad w_{i}=T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right)\end{equation}$
ここで、重みは正規化する必要があります：
$\begin{equation}\hat{w}_{i}=\frac{w_{i}}{\sum_{j=1}^{N_{c}} w_{j}}\end{equation}$

この重み $\hat{w}_{i}$ は、光線に沿った分割定数確率密度関数 (Piecewise-constant PDF) と見なすことができます。この確率密度関数を通じて、光線上の物体の分布を大まかに把握することができます。

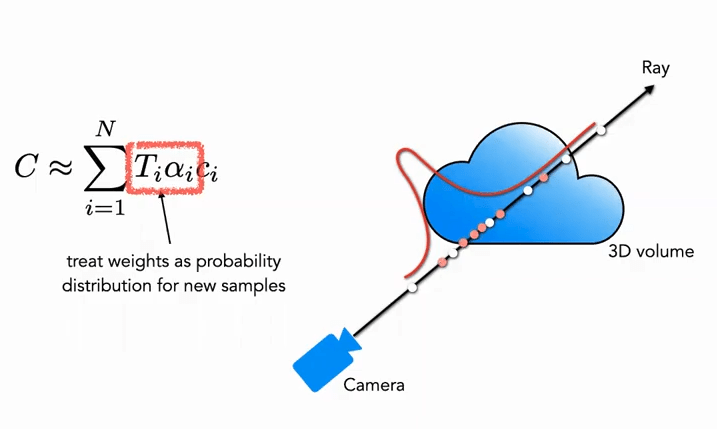
Fine 部分：第2段階では、逆変換サンプリング (Inverse Transform Sampling) を使用し、上記の分布に基づいて第2の集合 $N_f$ をサンプリングします。最終的には、式 (3) を使用して $\hat{C}_{f}(\mathbf{r})$ を計算しますが、異なる点は、すべての $N_c + N_f$ サンプルを使用することです。この方法を使用することで、2回目のサンプリングは分布に基づいて、実際にシーン内容がある領域でより多くのサンプルを取得し、重要度サンプリング (Importance Sampling) を実現します。

図のように、白い点は最初の均一サンプリングの点であり、白い均一サンプリング後に得られた分布に基づいて、2回目のサンプリングで赤い点がサンプリングされます。確率が高い場所では密に、確率が低い場所では疎にサンプリングされます（粒子フィルタに非常に似ています）。

3.3 Implementation Details (実装の詳細)

訓練損失関数に関しては、本論文の定義は非常にシンプルで直接的です。粗いネットワークと精密なネットワークの両方に対して、レンダリングの $L_2$ Loss を使用します。式は次の通りです：
$\begin{equation}\mathcal{L}=\sum_{\mathbf{r} \in \mathcal{R}}\left[\left\|\hat{C}_{c}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}+\left\|\hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}\right]\end{equation}$

その中で：

$\mathcal{R}$ はバッチ内のすべてのサンプリングされた光線の集合を表します
$C(\mathbf{r})$ は真値の RGB カラーを表します
$\hat{C}_{c}(\mathbf{r})$ は粗いネットワークが予測した RGB カラーを表します
$\hat{C}_{f}(\mathbf{r})$ は精密なネットワークが予測した RGB カラーを表します

4 Results (実験結果)

本論文では、多くの関連する研究と比較を行いました。例えば：

Neural Volumes (NV)：https://github.com/facebookresearch/neuralvolumes
Scene Representation Networks (SRN)：https://github.com/vsitzmann/scene-representation-networks
Local Light Field Fusion (LLFF)：https://github.com/Fyusion/LLFF

4.1 Datasets (データセット)

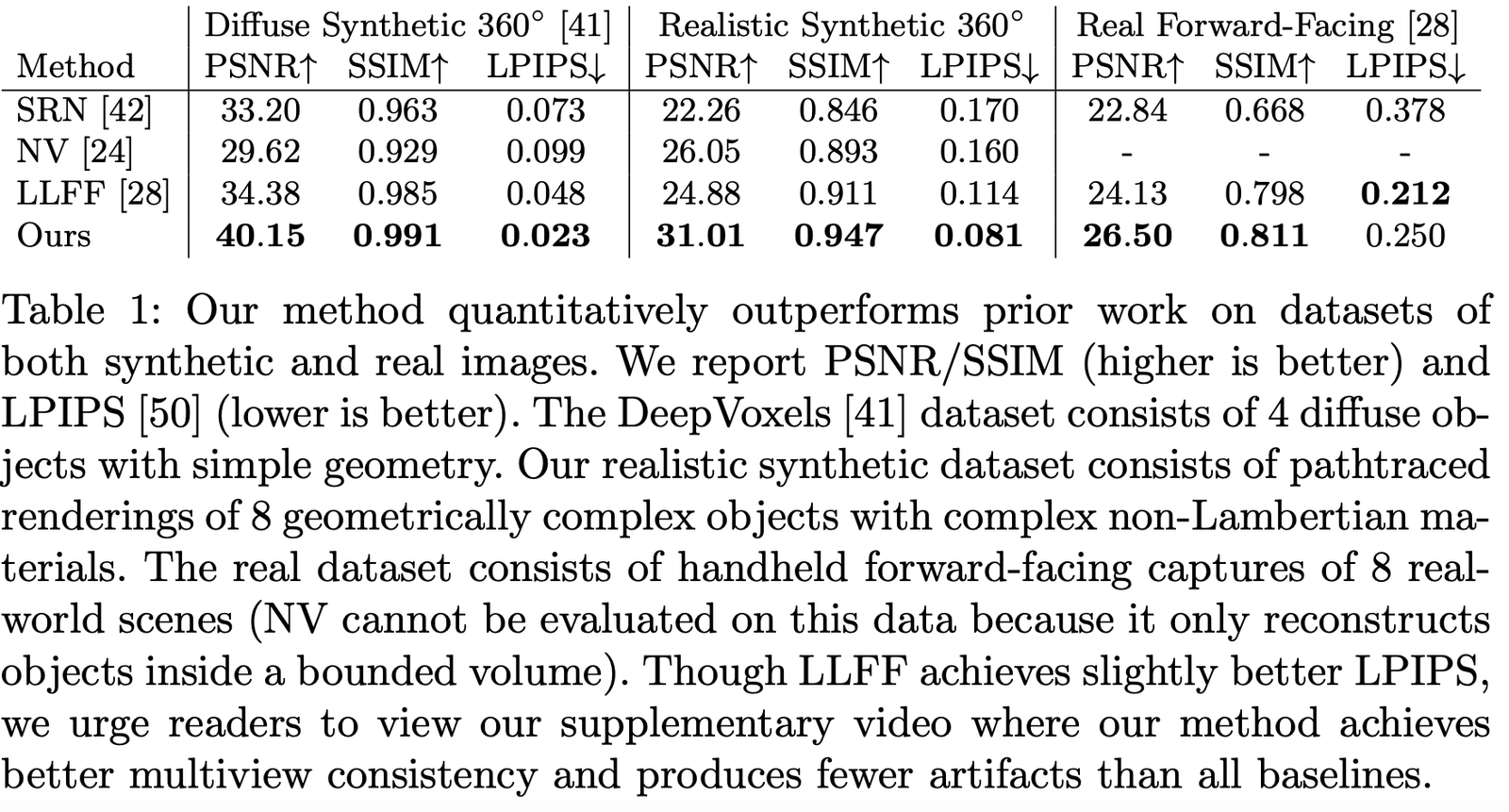
著者は異なるデータセットでのパフォーマンスを比較し、ほぼすべてのデータセットで圧倒的に優れていることがわかりました：

シミュレーションデータセットでの可視化結果：

実際のデータセットでの可視化結果：

4.2 Ablation Studies (アブレーションスタディ)

私たちは Realistic Synthetic 360◦ データセットで、異なるパラメータと設定の下でアブレーションスタディを行い、結果は次の通りです：

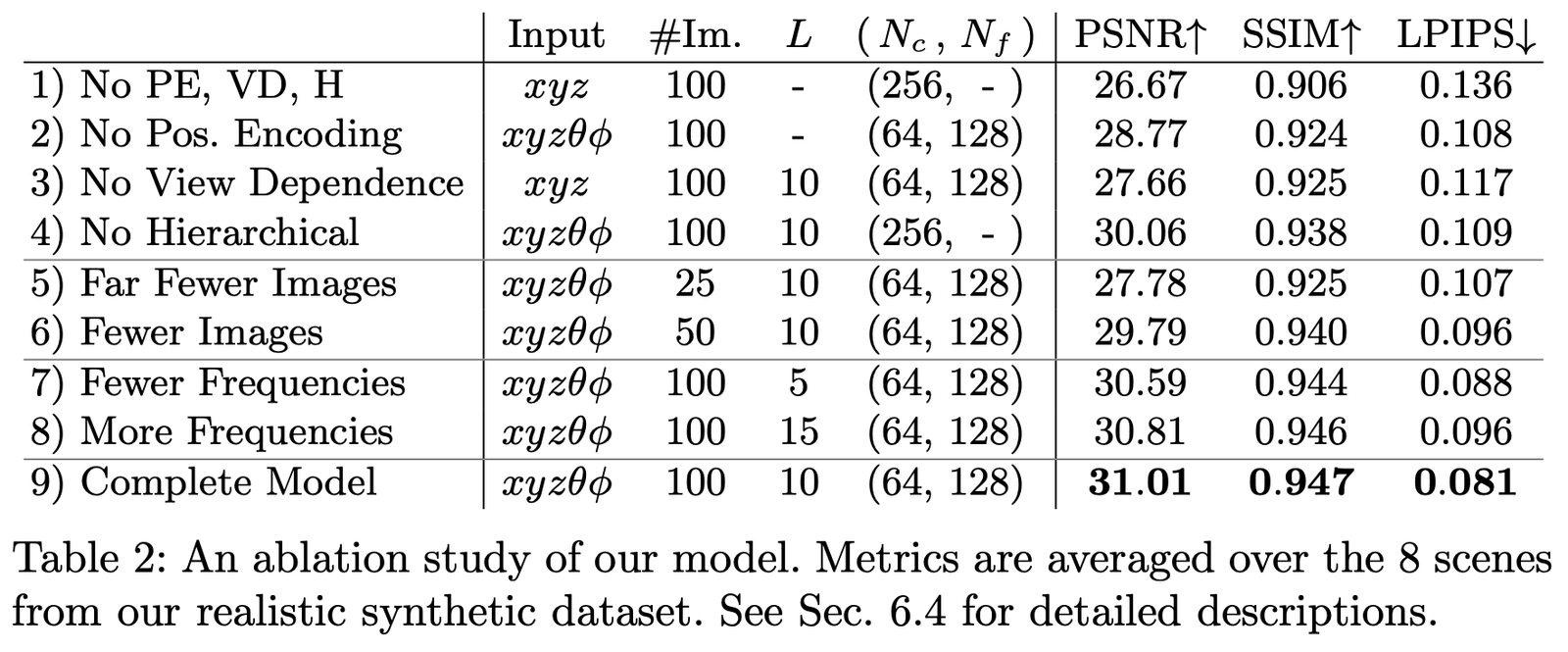
主に比較したのは次の設定です：

位置エンコーディング (PE)、すなわち $\mathbf{x}$
視点依存性 (VD)、すなわち $\mathbf{d}$
階層的サンプリング (H)

その中で：
第1行は上記のいずれの部分も含まない最小ネットワークを示します；
第2-4行はそれぞれ1つの部分を削除した場合を示します；
第5-6行はサンプル画像が少ない場合の効果の違いを示します；
第7-8行は周波数 $L$ （つまり位置エンコーディング $\mathbf{x}$ の周波数展開レベル）の設定が異なる場合の効果の違いを示します。

論文のまとめ

本論文の最大の革新点は、暗黙的表現を通じて、人工的に設計された三次元シーン表現の方法を回避し、より高次元からシーンの三次元情報を学習できる点です。しかし、欠点は非常に遅いということであり、この点は後続の多くの研究で改善されています。一方で、本論文の説明可能性や暗黙的表現の能力については、さらなる研究が必要です。
しかし、結局のところ、このようなシンプルで効果的な方法は、将来的に 3D および 4D シーン再構築の革命の一端を担い、三次元視覚に新たなブレイクスルーをもたらすと信じています。

論文のダウンロード

参考文献

[1] Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis[C]//European Conference on Computer Vision. Springer, Cham, 2020: 405-421.
[2] https://www.cnblogs.com/noluye/p/14547115.html
[3] https://www.cnblogs.com/noluye/p/14718570.html
[4] https://github.com/yenchenlin/awesome-NeRF
[5] https://zhuanlan.zhihu.com/p/360365941
[6] https://zhuanlan.zhihu.com/p/380015071
[7] https://blog.csdn.net/ftimes/article/details/105890744
[8] https://zhuanlan.zhihu.com/p/384946242
[9] https://zhuanlan.zhihu.com/p/386127288
[10] https://blog.csdn.net/g11d111/article/details/118959540
[11] https://www.bilibili.com/video/BV1fL4y1T7Ag
[12] https://zh.wikipedia.org/wiki/%E6%B8%B2%E6%9F%93%E6%96%B9%E7%A8%8B
[13] https://zhuanlan.zhihu.com/p/380015071
[14] https://blog.csdn.net/soaring_casia/article/details/117664146
[15] https://www.youtube.com/watch?v=Al6NTbgka1o
[16] https://github.com/matajoh/fourier_feature_nets

技术刘