NeRF est un Oral de l'ECCV 2020, ayant un impact très important, et on peut dire qu'il a créé une nouvelle voie pour la reconstruction de scènes basée sur l'expression implicite des réseaux neuronaux. En raison de sa simplicité conceptuelle et de ses résultats parfaits, de nombreux travaux liés à la 3D s'appuient encore sur cette base aujourd'hui.
La tâche que NeRF accomplit est la synthèse de nouvelles vues (Novel View Synthesis), c'est-à-dire l'observation d'une scène sous plusieurs angles connus (paramètres intrinsèques et extrinsèques de la caméra, images, pose, etc.) pour synthétiser des images sous n'importe quel nouvel angle. Dans les méthodes traditionnelles, cette tâche est généralement réalisée en reconstruisant d'abord la scène en 3D, puis en la rendant. NeRF, en revanche, cherche à obtenir directement l'image rendue sous un nouvel angle sans passer par une reconstruction explicite en 3D, en se basant uniquement sur les paramètres intrinsèques et extrinsèques. Pour atteindre cet objectif, NeRF utilise un réseau neuronal comme une représentation implicite d'une scène 3D, remplaçant les méthodes traditionnelles telles que les nuages de points, les maillages, les voxels, les TSDF, etc. Avec ce réseau, il est possible de rendre directement des images projetées sous n'importe quel angle et position.

L'idée de NeRF est relativement simple : il s'agit de rendre des voxels en intégrant les rayons de chaque pixel de l'image d'entrée en fonction de la densité (opacité), puis de comparer la valeur RGB rendue de ce pixel avec la valeur réelle comme perte (Loss). Comme le rendu voxel conçu dans l'article est entièrement différentiable, le réseau peut apprendre :

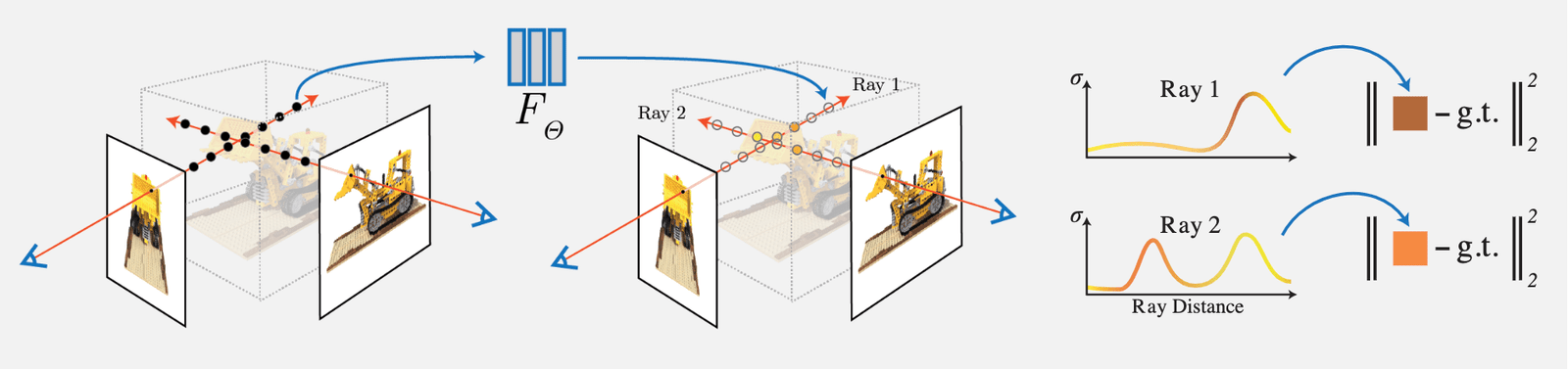
Les principaux travaux et points d'innovation sont les suivants :
1) Proposer une méthode pour représenter des scènes continues complexes de géométrie et de matériaux à l'aide d'un champ de radiance neuronal 5D (Neural Radiance Field), paramétré par un réseau MLP ;
2) Proposer une méthode de rendu différentiable améliorée basée sur le rendu volumétrique classique (Volume Rendering), permettant d'obtenir des images RGB via un rendu différentiable, et d'utiliser cela comme objectif d'optimisation. Cette partie inclut une stratégie d'accélération par échantillonnage hiérarchique, permettant de distribuer la capacité du MLP dans les zones de contenu visible ;
3) Proposer une méthode d'encodage de position (Position Encoding) pour mapper chaque coordonnée 5D dans un espace de dimension supérieure, ce qui permet d'optimiser le champ de radiance neuronal pour mieux exprimer les détails à haute fréquence.

1 Représentation de scène par champ de radiance neuronal (Neural Radiance Field Scene Representation)

NeRF représente une scène continue comme une fonction vectorielle à valeurs 5D, où :

• Entrée : position 3D \mathbf{x}=(x, y, z) et direction de vue 2D (\theta, \phi)
• Sortie : couleur émise \mathbf{c}=(r, g, b) et densité volumique (opacité) \sigma.

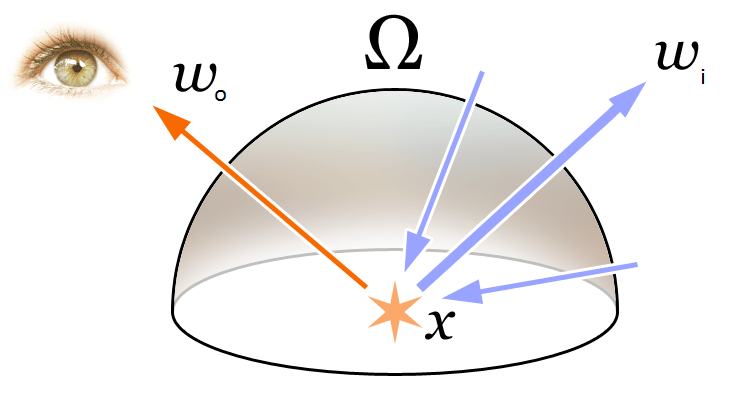
La direction de vue 2D peut être expliquée de manière intuitive par l'image ci-dessous :

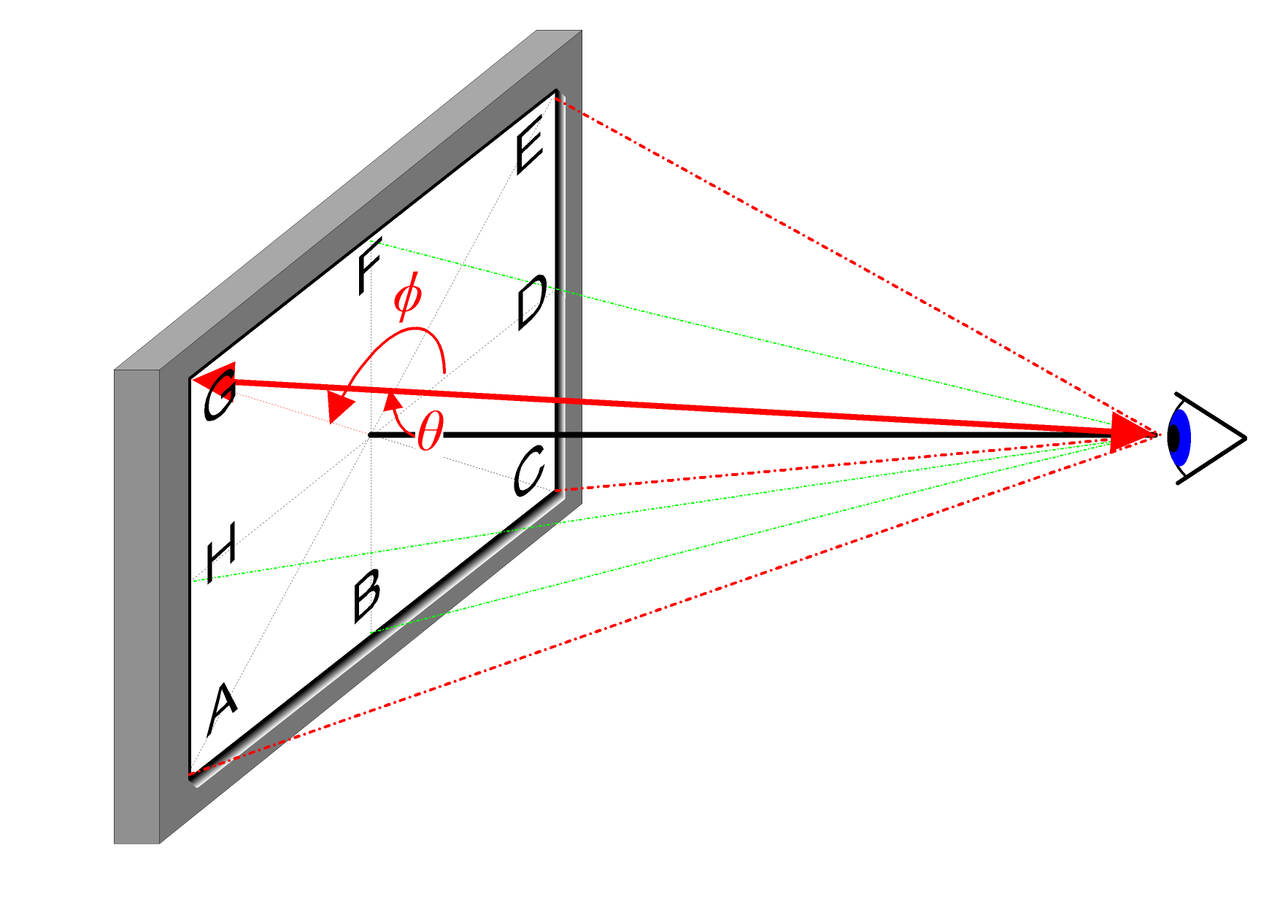
Dans la mise en œuvre réelle, la direction de vue est représentée par un vecteur unitaire dans un système de coordonnées cartésiennes 3D \mathbf{d}, c'est-à-dire la ligne reliant n'importe quelle position de l'image au centre optique de la caméra. Nous utilisons un réseau MLP entièrement connecté pour représenter cette correspondance :
\begin{equation}F_{\Theta}:(\mathbf{x}, \mathbf{d}) \rightarrow(\mathbf{c}, \sigma)\end{equation}

En optimisant les paramètres du réseau \Theta, on apprend cette correspondance entre une entrée de coordonnées 5D et une sortie de couleur et densité.

Pour permettre au réseau d'apprendre une représentation multi-vues, nous faisons deux hypothèses raisonnables :

• La densité volumique (opacité) \sigma ne dépend que de la position 3D \mathbf{x} et est indépendante de la direction de vue \mathbf{d}. La densité d'un objet à différentes positions ne devrait pas dépendre de l'angle d'observation, ce qui est assez évident.
• La couleur \mathbf{c} dépend à la fois de la position 3D \mathbf{x} et de la direction de vue \mathbf{d}.

La partie du réseau qui prédit la densité volumique \sigma prend uniquement la position \mathbf{x} en entrée, tandis que la partie qui prédit la couleur \mathbf{c} prend en entrée la direction de vue \mathbf{d}. En pratique :

• Le réseau MLP F_{\Theta} commence par 8 couches entièrement connectées (avec la fonction d'activation ReLU, chaque couche ayant 256 canaux), traitant les coordonnées 3D \mathbf{x}, pour obtenir \sigma et un vecteur de caractéristiques de 256 dimensions.
• Ce vecteur de caractéristiques de 256 dimensions est ensuite concaténé avec la direction de vue \mathbf{d}, et est alimenté dans une autre couche entièrement connectée (avec la fonction d'activation ReLU, chaque couche ayant 128 canaux), pour produire la couleur RGB dépendante de la direction.

La structure réseau schématique de cet article est illustrée ci-dessous :

La Fig 3 montre que notre réseau peut représenter des effets non lambertiens (non-Lambertian effects) ; la Fig 4 montre que si l'entrée de la dépendance à la vue (View Dependence) n'est pas utilisée lors de l'entraînement (seulement \mathbf{x}), le réseau ne peut pas représenter les effets de surbrillance.

2 Rendu volumétrique avec champs de radiance (Volume Rendering with Radiance Fields)

2.1 L'équation de rendu classique

Pour comprendre les concepts de Volume Rendering et de Radiance Field dans cet article, revenons d'abord à l'équation de rendu la plus fondamentale en infographie :
\begin{equation}\begin{array}{l}L_{o}(\boldsymbol{x}, \boldsymbol{d}) &=L_{e}(\boldsymbol{x}, \boldsymbol{d})+\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \left(\boldsymbol{\omega}_{i}, \boldsymbol{n}\right) d \boldsymbol{\omega}_{i}\\&=L_{e}(\boldsymbol{x}, \boldsymbol{d})+\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \cos \theta d \boldsymbol{\omega}_{i}\end{array}\end{equation}

Comme illustré ci-dessus, l'équation de rendu exprime la radiance (lumière émise) L_{o}(\boldsymbol{x}, \boldsymbol{d}) à une position \mathbf{x} dans une direction \mathbf{d}. Cette radiance est la somme de la lumière émise par le point lui-même L_{e}(\boldsymbol{x}, \boldsymbol{d}) et de la lumière réfléchie provenant de l'environnement. Plus précisément :

• L_{e}(\boldsymbol{x}, \boldsymbol{d}) représente la lumière émise par \mathbf{x} dans la direction \mathbf{d}
• \int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \cos \theta d \boldsymbol{\omega}_{i} représente l'intégrale sur l'hémisphère des directions incidentes
• f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) est la fonction de diffusion, qui exprime la proportion de lumière réfléchie de la direction incidente à la direction sortante.
• L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) est la lumière reçue depuis la direction \boldsymbol{\omega}_{i}
• \boldsymbol{n} est la normale à la position \mathbf{x} dans l'espace 3D, et \theta est l'angle entre \boldsymbol{\omega}_{i} et \boldsymbol{n}, avec \left(\boldsymbol{\omega}_{i}, \boldsymbol{n}\right)=\cos \theta

Pour comprendre simplement le concept de radiance : en physique, la lumière est une forme de rayonnement électromagnétique. Nous savons que la relation entre la longueur d'onde \lambda et la fréquence \nu est donnée par :
\begin{equation}c=\lambda \nu\end{equation}

Cela signifie que le produit des deux est la vitesse de la lumière c. Nous savons également que les couleurs RGB de la lumière visible sont le résultat de la radiation électromagnétique de différentes fréquences captée par la caméra. Ainsi, dans NeRF, le champ de radiance est considéré comme une modélisation approximative de la couleur.

2.2 Méthode classique de rendu volumétrique

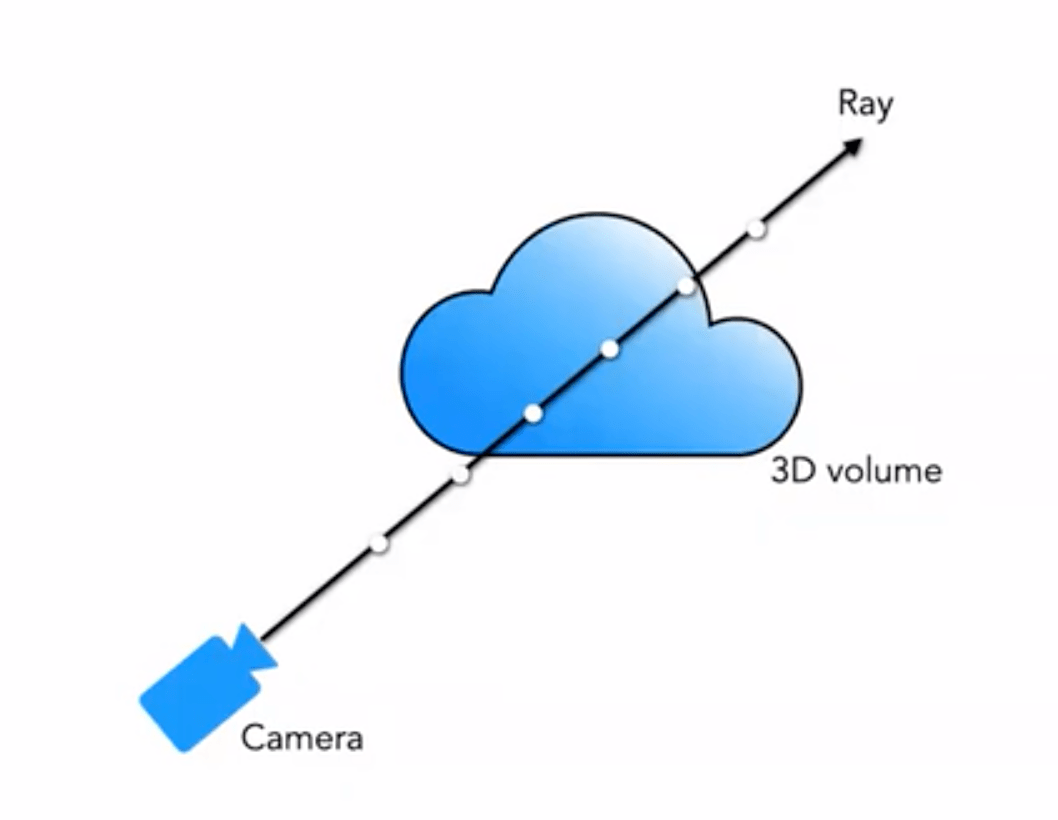
Nous rencontrons généralement des rendus avec des maillages ou des voxels. Pour de nombreux effets tels que les nuages, la fumée, etc., le rendu volumétrique est couramment utilisé :

Notre champ de radiance neuronal 5D représente la scène comme la densité volumique et la radiance directionnelle de n'importe quel point dans l'espace. La densité volumique \sigma(\mathbf{x}) est définie comme la probabilité différentielle qu'un rayon s'arrête à une particule infinitésimale à la position \mathbf{x} (ou peut être interprétée comme la probabilité qu'un rayon soit arrêté après avoir traversé ce point). En utilisant le principe classique du rendu volumétrique, nous pouvons rendre la couleur de n'importe quel rayon traversant la scène.

Ainsi, pour un rayon émis depuis une vue \mathbf{o} dans la direction \mathbf{d}, le point atteint à l'instant t est :
\begin{equation}\mathbf{r}(t)=\mathbf{o}+t \mathbf{d}\end{equation}
Alors, en intégrant la couleur le long de ce rayon dans l'intervalle (t_n, t_f), on obtient la valeur de couleur finale C(\mathbf{r}) :

La fonction T(t) représente la transparence accumulée (Accumulated Transmittance) du rayon de t_n à t. En d'autres termes, c'est la probabilité que le rayon traverse sans rencontrer de particules entre t_n et t. En suivant cette définition, le rendu de la vue est exprimé comme l'intégrale de C(\mathbf{r}), qui est la couleur obtenue par le rayon de la caméra traversant chaque pixel.

La fonction \sigma(\mathbf{x}) (La densité volumique \sigma(\mathbf{x}) peut être interprétée comme la probabilité différentielle qu’un rayon se termine à une particule infinitésimale à la position \mathbf{x}.)

2.3 Méthode de rendu volumétrique basée sur l'échantillonnage par segments

Cependant, dans le rendu réel, nous ne pouvons pas effectuer une intégration continue. Nous utilisons la méthode de quadrature pour résoudre numériquement l'intégrale. En adoptant un échantillonnage stratifié (stratified sampling) pour diviser l'intervalle \left[t_{n}, t_{f}\right] en sous-intervalles uniformément répartis, et en échantillonnant uniformément dans chaque sous-intervalle, la division est effectuée comme suit :
\begin{equation}t_{i} \sim \mathcal{U}\left[t_{n}+\frac{i-1}{N}\left(t_{f}-t_{n}\right), t_{n}+\frac{i}{N}\left(t_{f}-t_{n}\right)\right]\end{equation}

Pour les échantillons prélevés, nous utilisons une méthode d'intégration discrète :
\begin{equation}\hat{C}(\mathbf{r})=\sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}, \text { où } T_{i}=\exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right)\end{equation}
Où \delta_{i}=t_{i+1}-t_{i} est la distance entre les échantillons adjacents.

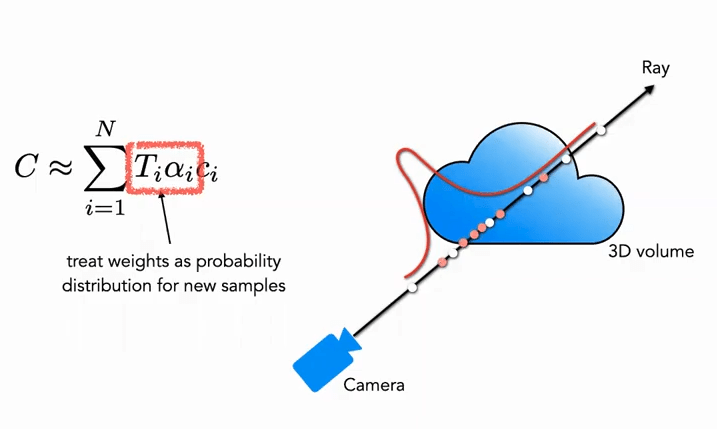
L'image ci-dessous illustre très bien le processus de rendu volumétrique :

3 Optimisation d'un champ de radiance neuronal (Optimizing a Neural Radiance Field)

La méthode décrite ci-dessus constitue le contenu de base de NeRF, mais les résultats obtenus ne sont pas optimaux, avec des problèmes tels que des détails insuffisamment précis et une vitesse d'entraînement lente. Pour améliorer encore la précision et la vitesse de reconstruction, nous introduisons deux stratégies supplémentaires :

• Encodage de position (Positional Encoding) : cette stratégie permet au MLP de mieux représenter les informations à haute fréquence, obtenant ainsi des détails plus riches ;
• Procédure d'échantillonnage hiérarchique (Hierarchical Sampling Procedure) : cette stratégie permet de mieux échantillonner les informations à haute fréquence de manière plus efficace pendant le processus d'entraînement.

3.1 Encodage de position (Positional Encoding)

Bien que les réseaux neuronaux puissent théoriquement approximer n'importe quelle fonction, il a été constaté expérimentalement que le MLP seul dans F_{\Theta} ne peut pas représenter pleinement les détails lorsqu'il traite les entrées (x, y, z, \theta, \phi). Cela correspond aux conclusions de Rahaman et al. (« On the spectral bias of neural networks. In: ICML (2018) »), qui ont montré que les réseaux neuronaux ont tendance à apprendre des fonctions à basse fréquence. Ils ont également montré que mapper les entrées à des espaces de dimension supérieure via des fonctions à haute fréquence permet de mieux ajuster les informations à haute fréquence dans les données.

En appliquant ces découvertes à la tâche de représentation de scènes par réseaux neuronaux, nous modifions F_{\Theta} en une composition de deux fonctions : F_{\Theta}=F_{\Theta}^{\prime} \circ \gamma, ce qui améliore considérablement les performances de représentation des détails. Où :

• \gamma est une fonction d'encodage qui mappe de \mathbb{R} à un espace de dimension supérieure \mathbb{R}^{2 L}
• F_{\Theta}^{\prime} est un réseau MLP classique

La fonction d'encodage utilisée dans cet article est la suivante :

La fonction \gamma(\cdot) sera appliquée aux coordonnées de position tridimensionnelles \mathbf{x} (normalisées à [-1, 1]) et aux coordonnées cartésiennes de la direction de vue tridimensionnelle \mathbf{d}. Dans cet article, pour \gamma(\mathbf{x}), nous fixons L=10 ; pour \gamma(\mathbf{d}), nous fixons L=4.

Ainsi, la longueur de l'encodage pour les coordonnées de position tridimensionnelles est : 3 \times 2 \times 10 = 60, et l'encodage de la position pour la direction de vue tridimensionnelle est 3 \times 2 \times 4 = 24, correspondant à la dimension d'entrée du schéma de réseau.

De manière similaire, il existe également une opération d'encodage de position dans le Transformer, mais elle est fondamentalement différente dans cet article. Dans le Transformer, l'encodage de position est utilisé pour représenter les informations séquentielles de l'entrée, tandis qu'ici, l'encodage de position est utilisé pour mapper l'entrée dans un espace de haute dimension afin que le réseau puisse mieux apprendre les informations de haute fréquence.

3.2 Procédure d'échantillonnage hiérarchique (分层采样方案)

La procédure d'échantillonnage hiérarchique provient des travaux d'accélération des algorithmes de rendu classiques. Dans la méthode de rendu volumétrique (Volume Rendering) mentionnée précédemment, la manière dont les points sont échantillonnés le long du rayon affecte l'efficacité finale. Si trop de points sont échantillonnés, l'efficacité du calcul est trop faible, mais si trop peu de points sont échantillonnés, l'approximation n'est pas suffisante. Une idée naturelle serait donc de concentrer l'échantillonnage autour des points qui contribuent le plus à la couleur et d'échantillonner plus faiblement autour des points qui contribuent moins, ce qui résoudrait le problème. Sur cette base, NeRF propose naturellement une procédure d'échantillonnage hiérarchique allant du grossier au fin (Coarse to Fine).

Partie Coarse : Tout d'abord, pour le réseau grossier, nous échantillonnons N_c points épars (c représentant Coarse), et modifions la formule (3) sous une nouvelle forme (en ajoutant des poids) :
\begin{equation}\hat{C}_{c}(\mathbf{r})=\sum_{i=1}^{N_{c}} w_{i} c_{i}, \quad w_{i}=T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right)\end{equation}
Où les poids doivent être normalisés :
\begin{equation}\hat{w}_{i}=\frac{w_{i}}{\sum_{j=1}^{N_{c}} w_{j}}\end{equation}

Les poids \hat{w}_{i} peuvent être considérés comme une fonction de densité de probabilité à segments constants le long du rayon (Piecewise-constant PDF). Grâce à cette fonction de densité de probabilité, on peut obtenir une distribution approximative des objets le long du rayon.

Partie Fine : Dans la deuxième phase, nous utilisons l'échantillonnage par transformation inverse (Inverse Transform Sampling), et échantillonnons un deuxième ensemble N_f basé sur la distribution obtenue précédemment. Finalement, nous utilisons toujours la formule (3) pour calculer \hat{C}_{f}(\mathbf{r}). Cependant, cette fois, nous utilisons tous les échantillons N_c + N_f. Avec cette méthode, le deuxième échantillonnage permet de concentrer davantage d'échantillons dans les zones contenant du contenu réel de la scène, réalisant ainsi un échantillonnage d'importance (Importance Sampling).

Comme illustré, les points blancs représentent les points échantillonnés uniformément lors de la première phase. Après cet échantillonnage uniforme, une distribution est obtenue, et lors de la deuxième phase, des points rouges sont échantillonnés en fonction de cette distribution, avec une densité plus élevée dans les zones à forte probabilité et une densité plus faible dans les zones à faible probabilité (cela ressemble beaucoup au filtrage particulaire).

3.3 Détails de l'implémentation (实现细节)

En ce qui concerne la fonction de perte d'entraînement, la définition dans cet article est très simple et directe : nous utilisons la perte L_2 rendue pour les réseaux grossier et fin, comme suit :
\begin{equation}\mathcal{L}=\sum_{\mathbf{r} \in \mathcal{R}}\left[\left\|\hat{C}_{c}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}+\left\|\hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}\right]\end{equation}

Où :

• \mathcal{R} représente l'ensemble des rayons échantillonnés dans un batch
• C(\mathbf{r}) représente la couleur RGB de vérité terrain
• \hat{C}_{c}(\mathbf{r}) représente la couleur RGB prédite par le réseau grossier
• \hat{C}_{f}(\mathbf{r}) représente la couleur RGB prédite par le réseau fin

4 Résultats (实验结果)

Cet article compare de nombreux travaux connexes, tels que :

• Neural Volumes (NV) : https://github.com/facebookresearch/neuralvolumes
• Scene Representation Networks (SRN) : https://github.com/vsitzmann/scene-representation-networks
• Local Light Field Fusion (LLFF) : https://github.com/Fyusion/LLFF

4.1 Jeux de données (数据集)

Les auteurs ont comparé les performances sur différents jeux de données, et il est évident que sur presque tous les jeux de données, les résultats sont largement en tête :

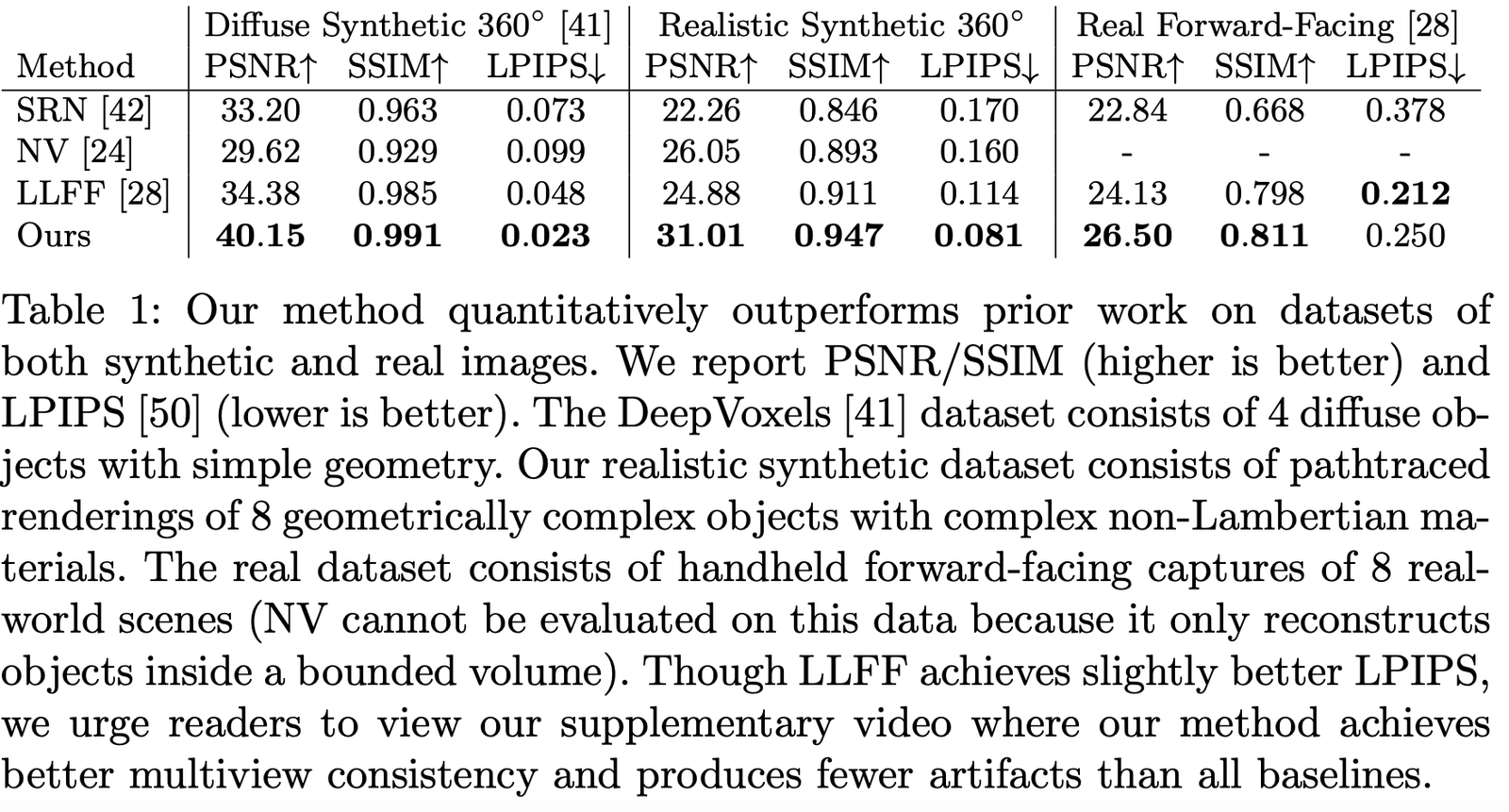
Visualisation des résultats sur des jeux de données simulés :

Visualisation des résultats sur des jeux de données réels :

4.2 Études d'ablation (消融实验)

Nous avons mené des études d'ablation avec différents paramètres et configurations sur le jeu de données Realistic Synthetic 360°, et les résultats sont les suivants :

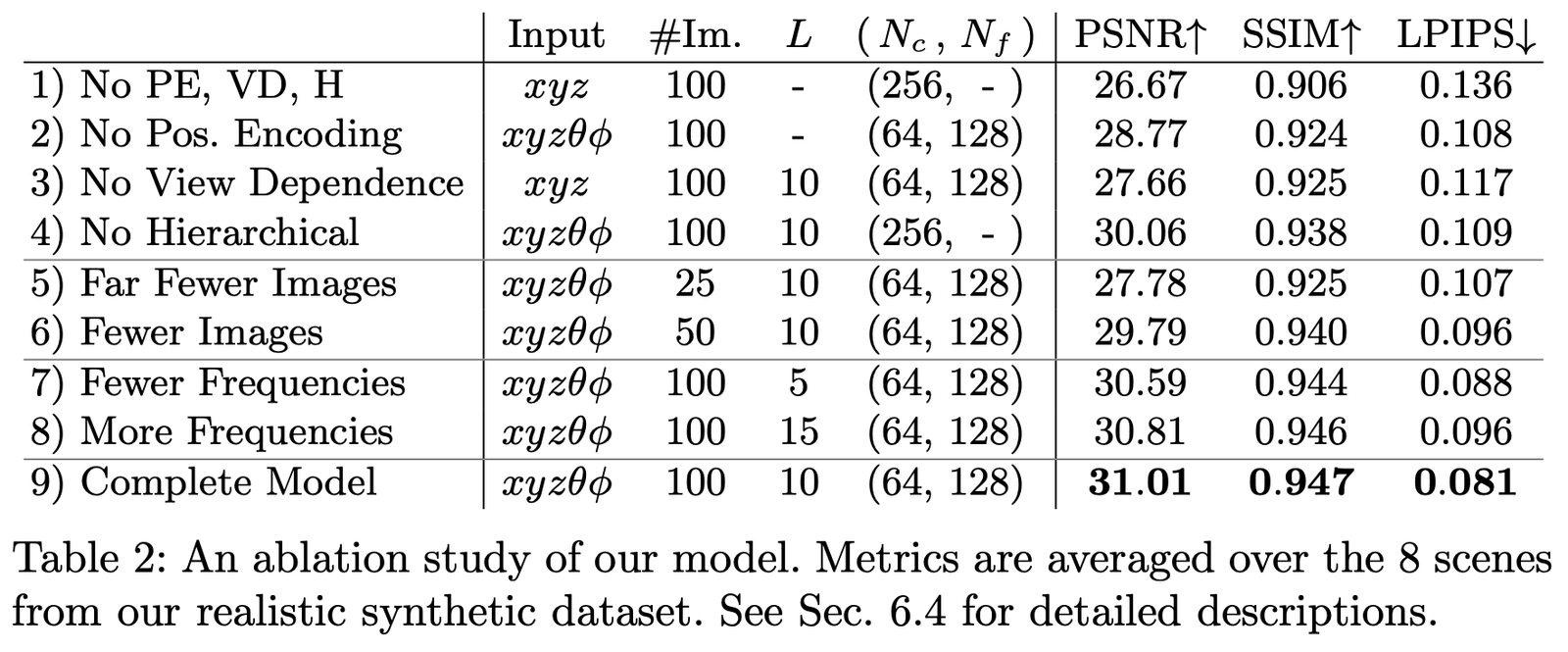
Les principales configurations comparées sont les suivantes :

• Encodage positionnel (PE), c'est-à-dire \mathbf{x}
• Dépendance à la vue (VD), c'est-à-dire \mathbf{d}
• Échantillonnage hiérarchique (H)

Où :
La première ligne représente le réseau minimal sans aucune des parties mentionnées ci-dessus ;
Les lignes 2 à 4 représentent la suppression d'une partie à la fois ;
Les lignes 5 à 6 montrent les différences de performance avec moins d'images d'échantillons ;
Les lignes 7 à 8 montrent les différences de performance avec des réglages de fréquence L (c'est-à-dire le niveau d'expansion fréquentielle de l'encodage positionnel \mathbf{x}).

Résumé de l'article

Le point d'innovation majeur de cet article est qu'il contourne les méthodes de représentation de scènes 3D conçues manuellement grâce à une représentation implicite, permettant d'apprendre des informations tridimensionnelles de la scène à partir de dimensions plus élevées. Cependant, l'inconvénient est que la vitesse est extrêmement lente, un point qui a été amélioré dans de nombreux travaux ultérieurs. D'autre part, l'interprétabilité de cet article et la capacité de la représentation implicite nécessitent encore plus de travail pour être explorées.
Mais en fin de compte, nous croyons que cette méthode simple et efficace deviendra une révolution dans la reconstruction de scènes 3D et 4D à l'avenir, apportant une nouvelle explosion à la vision tridimensionnelle.

Téléchargement de l'article

PDF | Site Web | Code (Officiel) | Code (Pytorch Lightning) | Enregistrement | Enregistrement (Bilibili)
Exemple Colab : Tiny NeRF | Full NeRF

Références

[1] Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis[C]//European Conference on Computer Vision. Springer, Cham, 2020: 405-421.
[2] https://www.cnblogs.com/noluye/p/14547115.html
[3] https://www.cnblogs.com/noluye/p/14718570.html
[4] https://github.com/yenchenlin/awesome-NeRF
[5] https://zhuanlan.zhihu.com/p/360365941
[6] https://zhuanlan.zhihu.com/p/380015071
[7] https://blog.csdn.net/ftimes/article/details/105890744
[8] https://zhuanlan.zhihu.com/p/384946242
[9] https://zhuanlan.zhihu.com/p/386127288
[10] https://blog.csdn.net/g11d111/article/details/118959540
[11] https://www.bilibili.com/video/BV1fL4y1T7Ag
[12] https://zh.wikipedia.org/wiki/%E6%B8%B2%E6%9F%93%E6%96%B9%E7%A8%8B
[13] https://zhuanlan.zhihu.com/p/380015071
[14] https://blog.csdn.net/soaring_casia/article/details/117664146
[15] https://www.youtube.com/watch?v=Al6NTbgka1o
[16] https://github.com/matajoh/fourier_feature_nets

Travaux connexes

DSNeRF : https://github.com/dunbar12138/DSNeRF (SfM accélère NerF)
BARF : https://github.com/chenhsuanlin/bundle-adjusting-NeRF
PlenOctrees : https://alexyu.net/plenoctrees/ (utilisation de PlenOctrees pour accélérer le rendu NeRF)
https://github.com/google-research/google-research/tree/master/jaxnerf (utilisation de JAX pour accélérer la vitesse d'entraînement)