论文笔记：NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

2021年11月1日

Table of Contents

NeRF 是 ECCV 2020 的 Oral，影响非常大，可以说从基础上创造出了新的基于神经网络隐式表达来重建场景的路线。由于其简洁的思想和完美的效果，至今仍然有非常多的 3D 相关工作以此为基础。
NeRF 所做的任务是 Novel View Synthesis（新视角合成），即在若干已知视角下对场景进行一系列的观测（相机内外参、图像、Pose 等），合成任意新视角下的图像。传统方法中，通常这一任务采用三维重建再渲染的方式实现，NeRF 希望不进行显式的三维重建过程，仅根据内外参直接得到新视角渲染的图像。为了实现这一目的，NeRF 使用用神经网络作为一个 3D 场景的隐式表达，代替传统的点云、网格、体素、TSDF 等方式，通过这样的网络可以直接渲染任意角度任意位置的投影图像。

NeRF 的思想比较简单，就是通过输入视角的图像每个像素的射线对于密度（不透明度）积分进行体素渲染，然后通过该像素渲染的 RGB 值与真值进行对比作为 Loss。由于文中设计的体素渲染是完全可微的，因此该网络可学习：

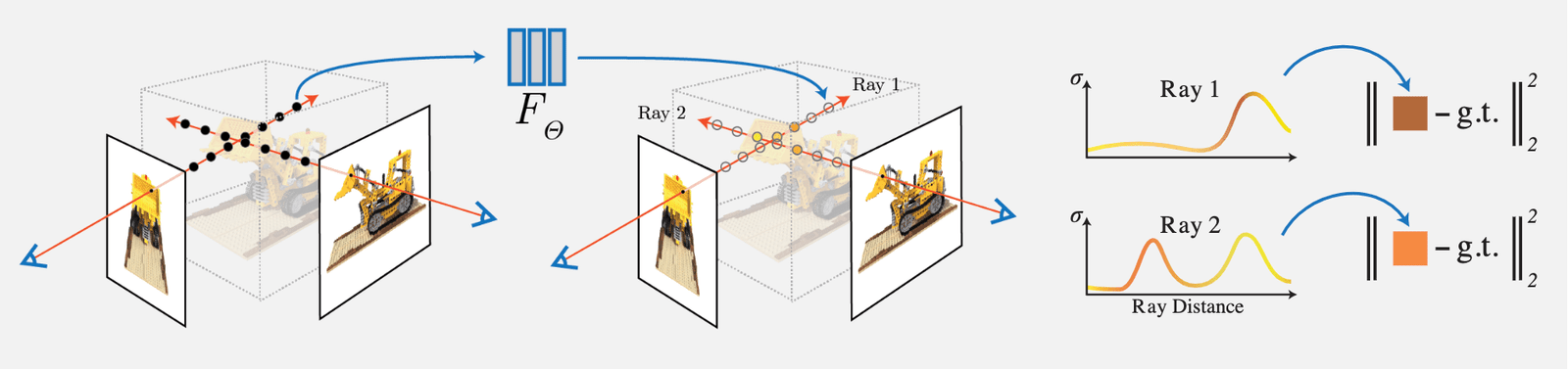
其主要工作和创新点如下：
1）提出一种用 5D 神经辐射场 (Neural Radiance Field) 来表达复杂的几何+材质连续场景的方法，该辐射场使用 MLP 网络进行参数化；
2）提出一种基于经典体素渲染 (Volume Rendering) 改进的可微渲染方法，能够通过可微渲染得到 RGB 图像，并将此作为优化的目标。该部分包含采用分层采样的加速策略，来将 MLP 的容量分配到可见的内容区域；
3）提出一种位置编码 (Position Encoding) 方法将每个 5D 坐标映射到更高维的空间，这样使得我们可以让我们优化神经辐射场更好地表达高频细节内容。

1 Neural Radiance Field Scene Representation (基于神经辐射场的场景表示)

NeRF 将一个连续的场景表示为一个 5D 向量值函数（vector-valued function），其中：

输入为：3D 位置 $\mathbf{x}=(x, y, z)$ 和 2D 视角方向 $(\theta, \phi)$
输出为：发射颜色 $\mathbf{c}=(r, g, b)$ 和体积密度（不透明度） $\sigma$ 。

对于其中的 2D 视角方向可以用下图进行直观解释：

在实际实现中，视角方向表示为一个三维笛卡尔坐标系单位向量 $\mathbf{d}$ ，也就是图像中的任意位置与相机光心的连线，我们用一个 MLP 全连接网络表示这种映射：
$\begin{equation}F_{\Theta}:(\mathbf{x}, \mathbf{d}) \rightarrow(\mathbf{c}, \sigma)\end{equation}$

通过优化这样一个网络的参数 $\Theta$ 来学习得到这样一个 5D 坐标输入到对应颜色和密度输出的映射。

为了让网络学习到多视角的表示，我们有如下两个合理假设：

体积密度（不透明度） $\sigma$ 只与三维位置 $\mathbf{x}$ 有关而与视角方向 $\mathbf{d}$ 无关。物体不同位置的密度应该和观察角度无关，这一点比较显然。
颜色 $\mathbf{c}$ 与三维位置 $\mathbf{x}$ 和视角方向 $\mathbf{d}$ 都相关。

预测体积密度 $\sigma$ 的网络部分输入仅仅是输入位置 $\mathbf{x}$ ，而预测颜色 $\mathbf{c}$ 的网络输入是视角和方向 $\mathbf{d}$ 。在具体实现上：

MLP 网络 $F_{\Theta}$ 首先用 8 层的全连接层（使用 ReLU 激活函数，每层有 256 个通道），处理 3D 坐标 $\mathbf{x}$ ，得到 $\sigma$ 和一个 256 维的特征向量。
将该 256 维的特征向量与视角方向 $\mathbf{d}$ 与视角方向一起拼接起来，喂给另一个全连接层（使用 ReLU 激活函数，每层有 128 个通道），输出方向相关的 RGB 颜色。

本文中一个示意的网络结构如下：

Fig 3 展示了我们的网络可以表示出非朗伯体效应（non-Lambertian effects）；Fig 4 展示了如果训练时没有视角 (View Dependence) 的输入（只有 $\mathbf{x}$ ），则网络无法表示高光效果。

2 Volume Rendering with Radiance Fields (基于辐射场的体素渲染)

2.1 经典渲染方程

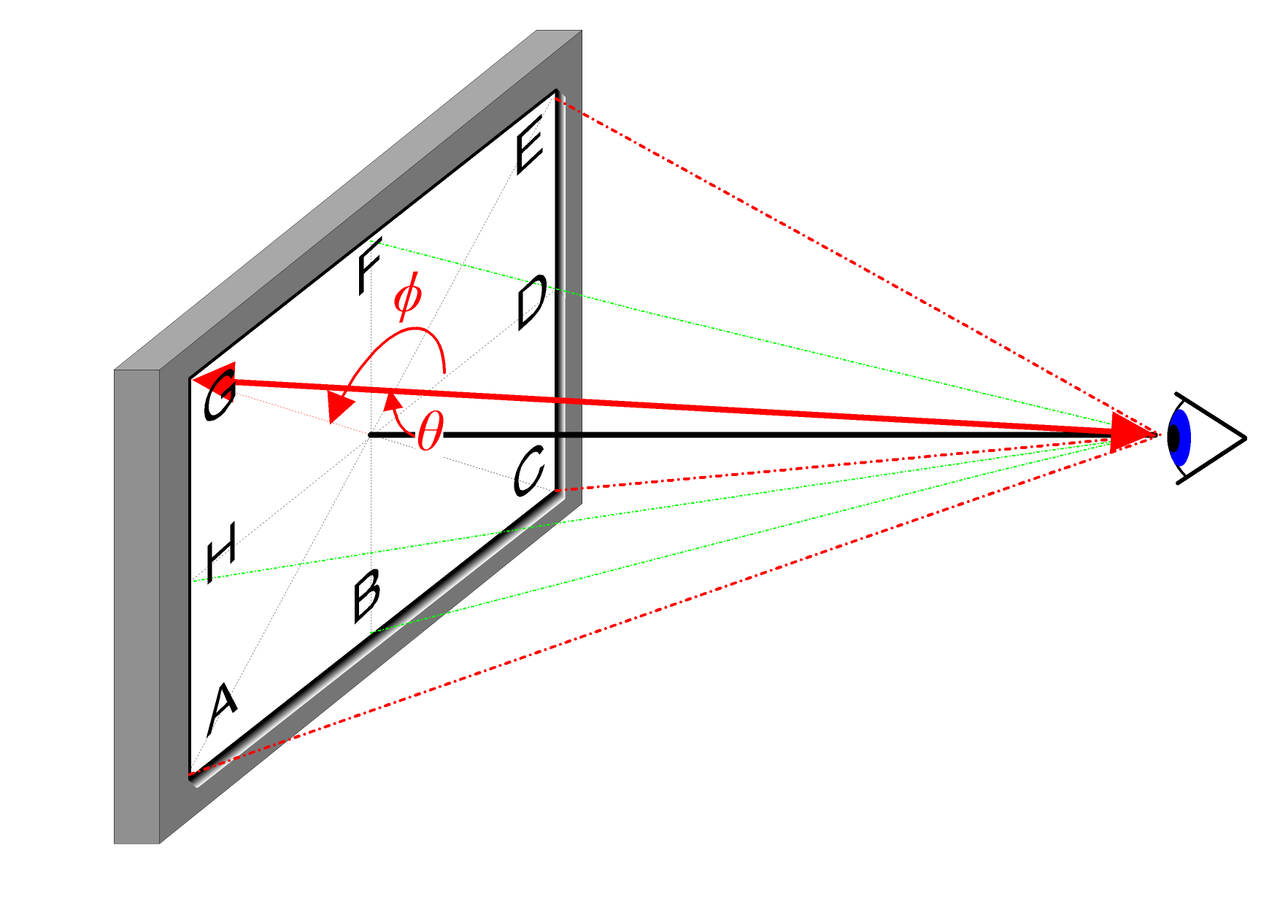
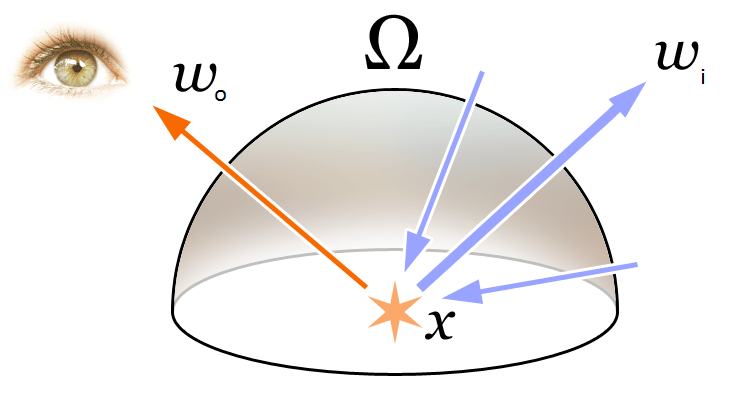
为了理解文中的 Volume Rendering 和 Radiance Field 的概念首先我们回顾下图形学中最基础的渲染方程：
$\begin{equation}\begin{array}{l}L_{o}(\boldsymbol{x}, \boldsymbol{d}) &=L_{e}(\boldsymbol{x}, \boldsymbol{d})+\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \left(\boldsymbol{\omega}_{i}, \boldsymbol{n}\right) d \boldsymbol{\omega}_{i}\\&=L_{e}(\boldsymbol{x}, \boldsymbol{d})+\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \cos \theta d \boldsymbol{\omega}_{i}\end{array}\end{equation}$

如上图所示，渲染方程表达了 3D 空间位置 $\mathbf{x}$ 在方向 $\mathbf{d}$ 的辐射（出射光） $L_{o}(\boldsymbol{x}, \boldsymbol{d})$ 。该辐射表达为该点自身向外的辐射（发射光） $L_{e}(\boldsymbol{x}, \boldsymbol{d})$ 和该点反射外界的辐射（反射光）之和。具体说来：

$L_{e}(\boldsymbol{x}, \boldsymbol{d})$ 表示 $\mathbf{x}$ 为光源点在方向 $\mathbf{d}$ 释放的辐射（发射光）
$\int_{\Omega} f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right) L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right) \cos \theta d \boldsymbol{\omega}_{i}$ 表示是入射方向半球的积分
$f_{r}\left(\boldsymbol{x}, \boldsymbol{d}, \boldsymbol{\omega}_{i}\right)$ 是散射函数，表示在该点从入射方向到出射方向辐射的反射比例。
$L_{i}\left(\boldsymbol{x}, \boldsymbol{\omega}_{i}\right)$ 是从 $\boldsymbol{\omega}_{i}$ 方向接收到的辐射
$\boldsymbol{n}$ 是 3D 空间位置 $\mathbf{x}$ 的法向，而 $\theta$ 是 $\boldsymbol{\omega}_{i}$ 与 $\boldsymbol{n}$ 的夹角，显然有 $\left(\boldsymbol{\omega}_{i}, \boldsymbol{n}\right)=\cos \theta$

简单理解辐射概念，在物理学中，光就是电磁辐射，我们知道电磁波长 $\lambda$ 与频率 $\nu$ 的关系式为：
$\begin{equation}c=\lambda \nu\end{equation}$

也就是二者的乘积为光速 $c$ 。而我们又知道可见光的颜色 RGB 就是不同频率的光辐射作用于相机的结果。因此在 NeRF 中认为辐射场就是对于颜色的近似建模。

2.2 经典的体素渲染方法

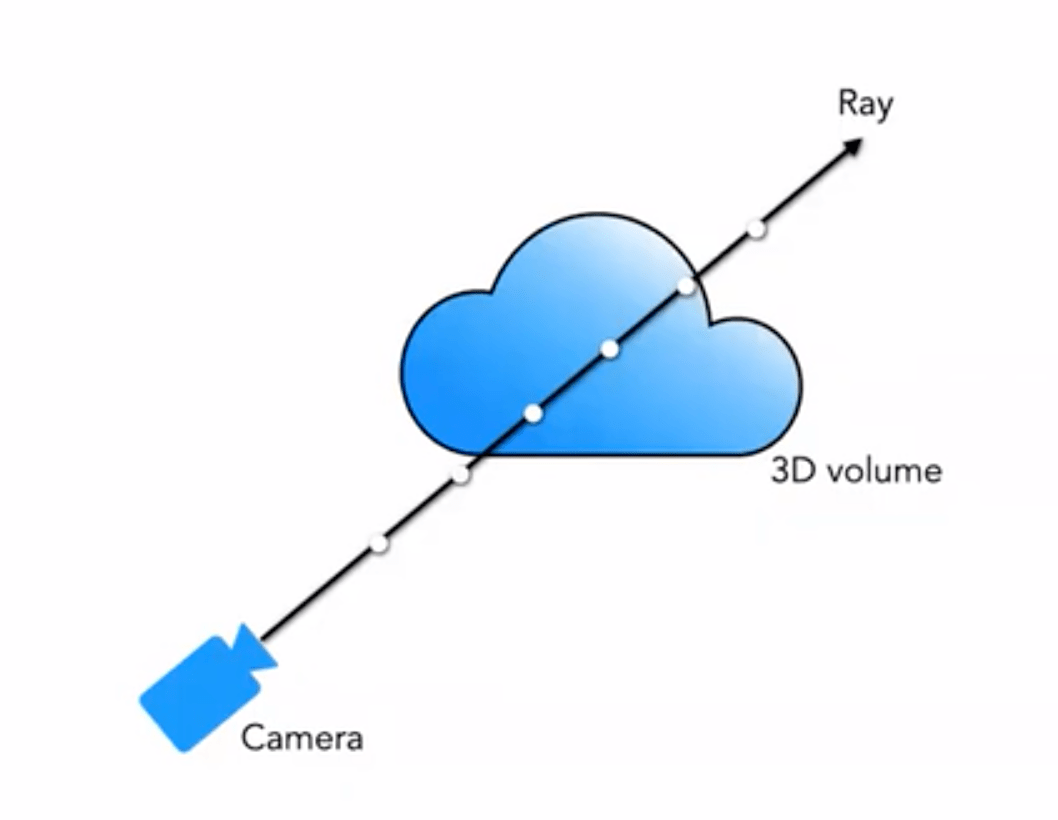
我们通常接触的是渲染有网格渲染、体素渲染等，对于很多类似云彩、烟尘等等特效，常用的就是体素渲染：

我们的 5D 神经辐射场将场景表示为：其所在空间中任意点的体素密度和有方向的辐射亮度。体素密度 $\sigma(\mathbf{x})$ 定义为光线停留在位置 $\mathbf{x}$ 处无穷小粒子的可导概率（或者也可以理解为光线穿过此点后终止的概率）。使用经典的立体渲染的原理，我们可以渲染出任意射线穿过场景的颜色。

因此对于某个视角 $\mathbf{o}$ 发出的方向为 $\mathbf{d}$ 的光线，其在 $t$ 时刻到达点为：
$\begin{equation}\mathbf{r}(t)=\mathbf{o}+t \mathbf{d}\end{equation}$
那么沿这个方向在范围 $(t_n, t_f)$ 对颜色积分，获得最终的颜色值 $C(\mathbf{r})$ 为：

\begin{equation}C(\mathbf{r})=\int_{t_{n}}^{t_{f}} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_{n}}^{t} \sigma(\mathbf{r}(s)) d s\right)\end{equation}

函数 $T(t)$ 表示光线从 $t_n$ 到 $t$ 累积的透明度 (Accumulated Transmittance)。换句话说，就是光线从 $t_n$ 到 $t$ 穿过没有碰到任何粒子的概率。按照这个定义，视图的渲染就是表示成对于 $C(\mathbf{r})$ 的积分，它是就是虚拟相机穿过每个像素的相机光线，所得到的颜色。

函数 $\sigma(\mathbf{x})$ （The volume density $\sigma(\mathbf{x})$ can be interpreted as the differential probability of a
ray terminating at an infinitesimal particle at location $\mathbf{x}.$ ）

Ray casting for volume rendering (© Zhanping Liu).

2.3 基于分段采样近似的体素渲染方法

不过在实际的渲染中，我们并不能进行连续积分，我们使用求积法（quadrature）进行积分的数值求解。通过采用分层采样 (stratified sampling) 的方式对 $\left[t_{n}, t_{f}\right]$ 划分成均匀分布的小区间，对每个区间进行均匀采样，划分的方式如下：
$\begin{equation}t_{i} \sim \mathcal{U}\left[t_{n}+\frac{i-1}{N}\left(t_{f}-t_{n}\right), t_{n}+\frac{i}{N}\left(t_{f}-t_{n}\right)\right]\end{equation}$

对于采样的样本，我们采用离散的积分方法：
$\begin{equation}\hat{C}(\mathbf{r})=\sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}, \text { where } T_{i}=\exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right)\end{equation}$
其中， $\delta_{i}=t_{i+1}-t_{i}$ 是相邻样本之间的距离。

下图非常形象地演示了体素渲染的流程：

3 Optimizing a Neural Radiance Field (优化一个神经辐射场)

上述方法就是 NeRF 的基本内容，但基于此得到的结果并能达到最优效果，存在例如细节不够精细、训练速度较慢等问题。为了进一步提升重建精度和速度，我们还引入了下面两个策略：

Positional Encoding (位置编码)：通过这一策略，能够使得 MLP 更好地表示高频信息，从而得到丰富的细节；
Hierarchical Sampling Procedure (金字塔采样方案)：通过这一策略，能够使得训练过程更高效地采样高频信息。

3.1 Positional Encoding (位置编码)

尽管神经网络理论上可以逼近任何函数，但是通过实验发现仅用 MLP 构成的 $F_{\Theta}$ 处理输入 $(x, y, z, \theta, \phi)$ 不能够完全表示出细节。这和 Rahaman 等人工作（《On the spectral bias of neural networks. In: ICML (2018) 》）所证明的结论相符，即：神经网络倾向于学习到频率较低的函数。同时他们的工作也表明，通过将输入通过高频函数映射到高维空间中，可以更好地拟合数据中的高频信息。

通过这些发现应用到神经网络场景表达任务中，我们将 $F_{\Theta}$ 修改成两个函数的组合： $F_{\Theta}=F_{\Theta}^{\prime} \circ \gamma$ ，通过这样的方式可以明显提升细节表达的性能，其中：

$\gamma$ 表示从 $\mathbb{R}$ 到更高维 $\mathbb{R}^{2 L}$ 的编码函数
$F_{\Theta}^{\prime}$ 是正常的 MLP 网络

本文使用的编码函数如下：

\begin{equation}\gamma(p)=\left(\sin \left(2^{0} \pi p\right), \cos \left(2^{0} \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)\end{equation}

该函数 $\gamma(\cdot)$ 会应用于三维位置坐标 $\mathbf{x}$ （归一化到 $[-1, 1]$ ）和三维视角方向笛卡尔坐标 $\mathbf{d}$ 。在本文中对于 $\gamma(\mathbf{x})$ 设置 $L=10$ ；对于 $\gamma(\mathbf{d})$ 设置 $L=4$ 。

因此可以得到对于三维位置坐标的编码长度为： $3 \times 2 \times 10 = 60$ ，对于三维视角方向的位置编码为 $3 \times 2 \times 4 = 24$ ，与网络结构图上的输入维度相对应。

相似地，在 Transformer 中也有一个类似的位置编码操作，不过本文中与其还是根本不同。在 Transformer 中位置编码是用来表示输入的序列信息的，而这里的位置编码是做用于输入将输入映射到高维从而让网络能够更好地学习到高频信息。

3.2 Hierarchical Sampling Procedure (分层采样方案)

分层采样方案来自于经典渲染算法的加速工作，在前述的体素渲染 (Volume Rendering) 方法中，对于射线上的点如何采样会影响最终的效率，如果采样点过多计算效率太低，采样点过少又不能很好地近似。那么一个很自然的想法就是希望对于颜色贡献大的点附近采样密集，贡献小的点附近采样稀疏，这样就可以解决问题。基于这一想法，NeRF 很自然地提出由粗到细的分层采样方案（Coarse to Fine）。

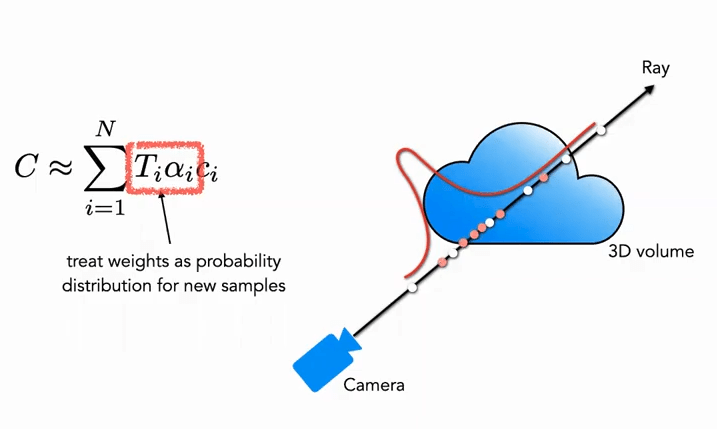
Coarse 部分：首先对于粗网络，我们采样 $N_c$ 个稀疏点（c 表示 Coarse），并将公式 (3) 用新的形式修改（加入权重）：
$\begin{equation}\hat{C}_{c}(\mathbf{r})=\sum_{i=1}^{N_{c}} w_{i} c_{i}, \quad w_{i}=T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right)\end{equation}$
其中权重需要进行归一化：
$\begin{equation}\hat{w}_{i}=\frac{w_{i}}{\sum_{j=1}^{N_{c}} w_{j}}\end{equation}$

这里面的权重 $\hat{w}_{i}$ 可以看成沿着射线的分段常数概率密度函数 (Piecewise-constant PDF)。通过这个概率密度函数可以粗略地得到射线上物体的分布情况。

Fine 部分：在第二阶段，我们使用逆变换采样 (Inverse Transform Sampling)，根据上面的分布采样出第二个集合 $N_f$ ，最终我们仍然使用公式 (3) 来计算 $\hat{C}_{f}(\mathbf{r})$ 。但不同的是使用了全部的 $N_c + N_f$ 个样本。使用这种方法，第二次采样可以根据分布采样更多的样本在真正有场景内容的区域，实现了重要性抽样 (Importance Sampling)。

如图所示，白色点为第一次均匀采样的点，通过白色均匀采样后得到的分布，第二次再根据分布对进行红色点采样，概率高的地方密集，概率低的地方稀疏 (很像粒子滤波)。

3.3 Implementation Details (实现细节)

在训练损失函数方面，本文的定义非常简单直接，就是对于粗网络和精网络都用渲染的 $L_2$ Loss，公式如下：
$\begin{equation}\mathcal{L}=\sum_{\mathbf{r} \in \mathcal{R}}\left[\left\|\hat{C}_{c}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}+\left\|\hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}\right]\end{equation}$

其中：

$\mathcal{R}$ 表示一个 batch 中的所有采样的射线集合
$C(\mathbf{r})$ 表示真值的 RGB 颜色
$\hat{C}_{c}(\mathbf{r})$ 表示 Coarse 网络预测的 RGB 颜色
$\hat{C}_{f}(\mathbf{r})$ 表示 Fine 网络预测的 RGB 颜色

4 Results (实验结果)

本文对比了很多相关的工作例如：

Neural Volumes (NV)：https://github.com/facebookresearch/neuralvolumes
Scene Representation Networks (SRN)：https://github.com/vsitzmann/scene-representation-networks
Local Light Field Fusion (LLFF)：https://github.com/Fyusion/LLFF

4.1 Datasets (数据集)

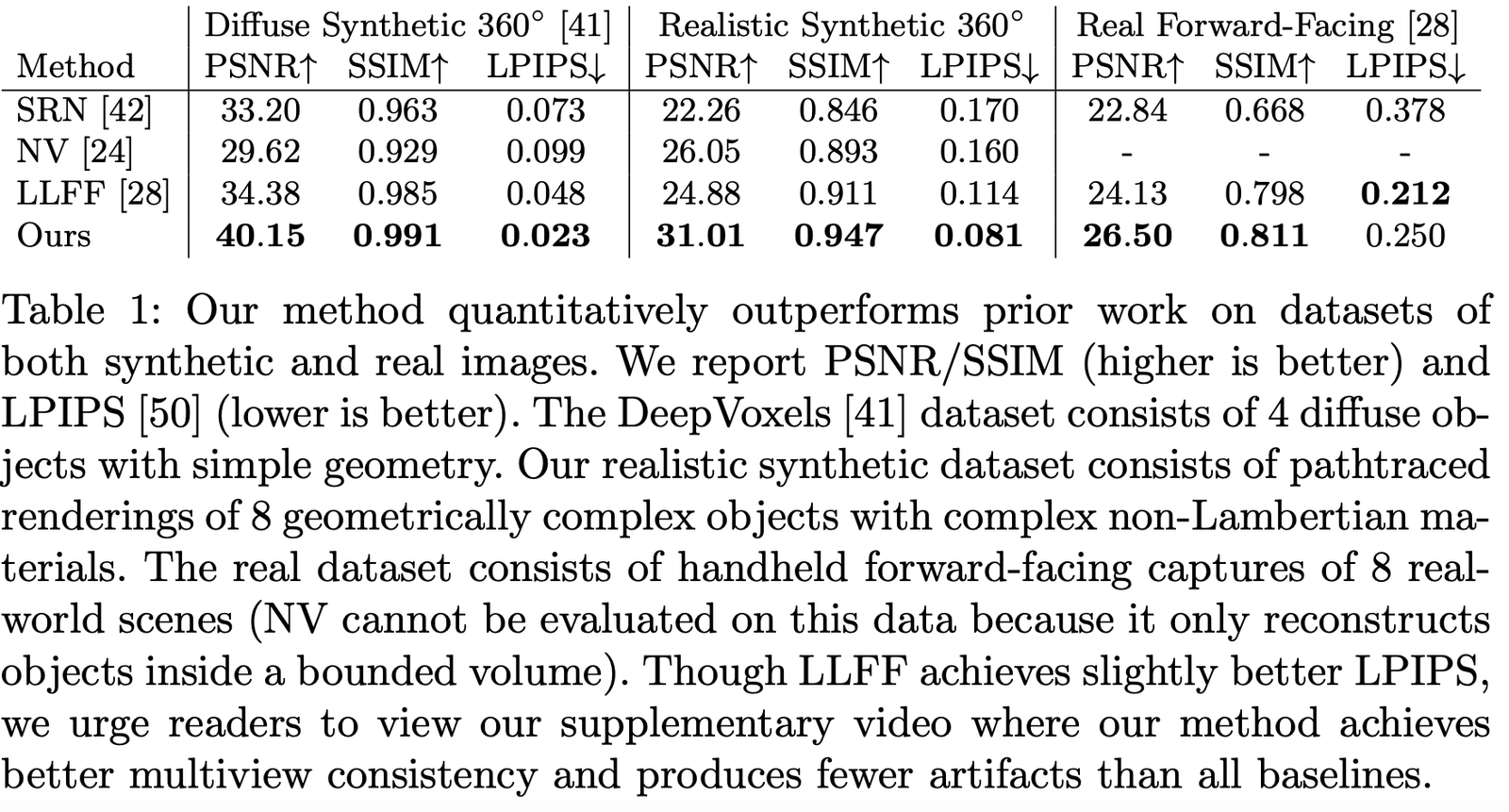
作者对比了在不同数据集中的表现，可以看出基本上所有数据集上都是遥遥领先的：

在仿真数据集上的可视化效果：

在真实数据集上的可视化效果：

4.2 Ablation Studies (消融实验)

我们在数据集 Realistic Synthetic 360◦ 上进行了不同参数和设置下的消融实验，结果如下：

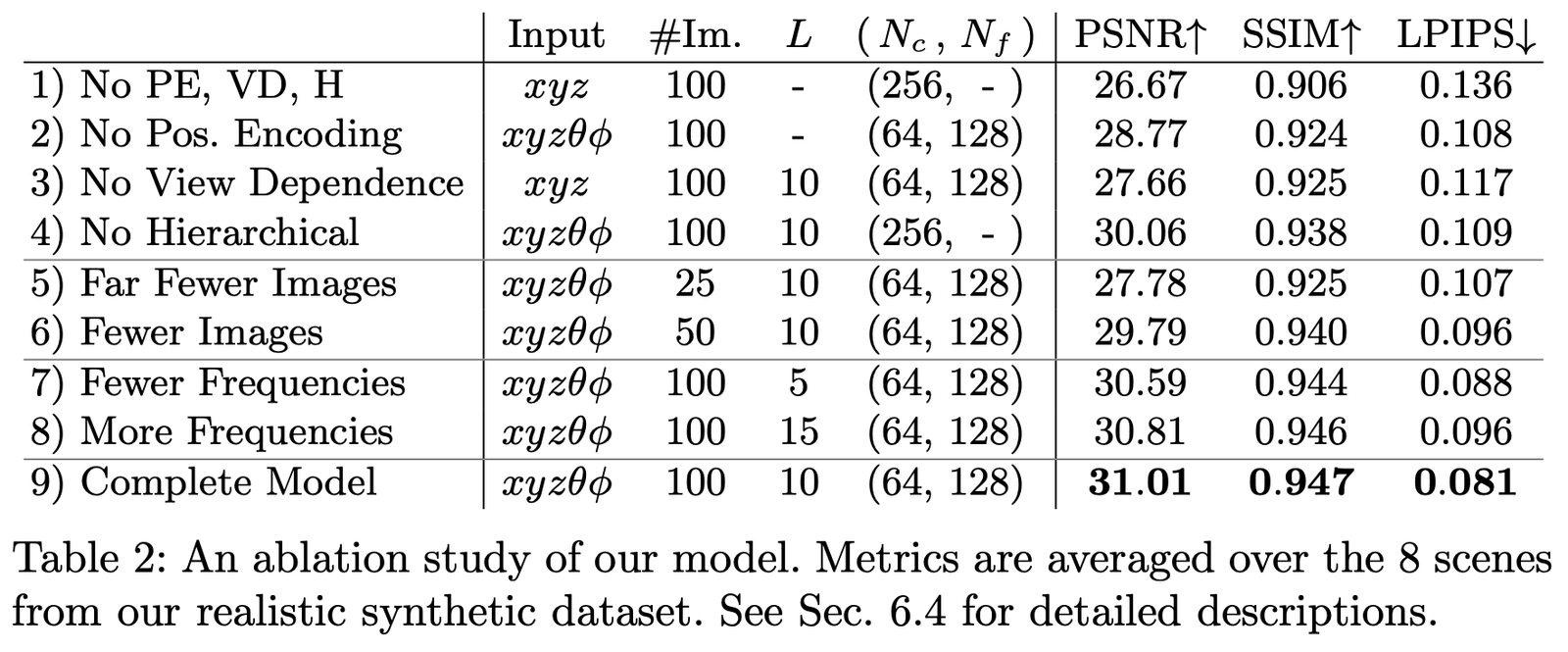
主要对比的是如下几个设置：

Positional encoding (PE)，即 $\mathbf{x}$
View Dependence (VD)，即 $\mathbf{d}$
Hierarchical sampling (H)

其中：
第1行表示不包含以上任何一个部分的最小网络；
第2-4行表示每次分别去掉一个部分；
第5-6行表示样本图像更少时的效果差异；
第7-8行表示频率 $L$ （也就是位置编码 $\mathbf{x}$ 的频率展开级别）设置不同时的效果差异。

论文小结

本文最大的创新点就是通过隐式表达绕过了人工设计三维场景表示的方法，能够从更高维度学习到场景的三维信息。但缺点是速度非常慢，这一点在后续很多工作也有改进。另一方面本文的可解释性，隐式表达的能力，依然需要更多工作来探索。
但归根结底，相信这样简洁有效的方式，未来会成为 3D 和 4D 场景重建的革命点，给三维视觉带来新的爆发。

论文下载

参考材料

[1] Mildenhall B, Srinivasan P P, Tancik M, et al. Nerf: Representing scenes as neural radiance fields for view synthesis[C]//European Conference on Computer Vision. Springer, Cham, 2020: 405-421.
[2] https://www.cnblogs.com/noluye/p/14547115.html
[3] https://www.cnblogs.com/noluye/p/14718570.html
[4] https://github.com/yenchenlin/awesome-NeRF
[5] https://zhuanlan.zhihu.com/p/360365941
[6] https://zhuanlan.zhihu.com/p/380015071
[7] https://blog.csdn.net/ftimes/article/details/105890744
[8] https://zhuanlan.zhihu.com/p/384946242
[9] https://zhuanlan.zhihu.com/p/386127288
[10] https://blog.csdn.net/g11d111/article/details/118959540
[11] https://www.bilibili.com/video/BV1fL4y1T7Ag
[12] https://zh.wikipedia.org/wiki/%E6%B8%B2%E6%9F%93%E6%96%B9%E7%A8%8B
[13] https://zhuanlan.zhihu.com/p/380015071
[14] https://blog.csdn.net/soaring_casia/article/details/117664146
[15] https://www.youtube.com/watch?v=Al6NTbgka1o
[16] https://github.com/matajoh/fourier_feature_nets

技术刘